J. Piaget et la psychologie du développement cognitif (XII) – CEPIAG

Posted on 31 mars 201221 février 2013 by Jean-Jacques Ducret

Dernier survol…

[Vers: Cours n. 11 — Cours n. 10 — Cours n. 9 — Cours n. 8 — Cours n. 7 — Cours n. 6 — Cours n. 5 — Cours n. 4 — Cours n. 3 — Cours n. 2 — Cours n. 1]

Préambule

Les 12 cours que j’ai été invité à donner ce semestre avaient pour objectif fort ambitieux de permettre aux étudiantes et étudiants d’atteindre une vue d’ensemble de la psychologie du développement cognitif telle que l’a conçue et développée Piaget dès le début des années 1920 jusqu’à la fin des années 1970. Mais d’emblée nous avons signalé que cette psychologie —qui encore aujourd’hui reste un élément clé de notre compréhension de l’intelligence humaine et une source d’inspiration pour des chercheurs du monde entier— ne peut être correctement appréhendée que si l’on a par ailleurs en vue son insertion dans la totalité de l’œuvre piagétienne, dont elle n’est qu’une composante, certes centrale. Bien entendu, face à l’ampleur de cette œuvre, il était hors de question d’examiner toutes les autres composantes, et même, sur terrain de la psychologie, d’aborder l’ensemble des sous-domaines pour lesquels des recherches approfondies ont été faites, pour la plupart en utilisant la même méthode que celle que nous avons vue à l’œuvre dans l’étude de la progression de la pensée et des notions logico-mathématiques. Au cours de notre présentation, nous avons néanmoins insisté sur le lien indissociable de la psychologie piagétienne du développement avec le questionnement épistémologique sans lequel son auteur n’aurait à coup sûr pu éclairer la nature cachée de l’intelligence humaine (il suffit pour le démontrer de comparer les travaux de Piaget sur la psychologie du nombre ou de la pensée logique avec ceux d’auteurs tels que Binet, Janet, Vygotski, pour ne pas citer des auteurs contemporains qui, faute d’une connaissance approfondie des études sur le fondement des sciences logiques et mathématiques, passent largement à côté de ce que peut bien signifier le nombre, la pensée logique, l’espace, le temps, les quantités physiques et même la notion d’objet, toutes notions constitutives de l’intelligence, à des étapes différentes de sa genèse et de leur genèse chez l’enfant et l’adolescent).

Par ailleurs, nous avons signalé, sans approfondir, que, nourri par sa profonde connaissance de la philosophie, Piaget ne s’est pas limité à résoudre le problème épistémologique de l’origine et de la nature de l’intelligence et des connaissances humaines. Au-delà de ce noyau, c’est la raison toute entière, c’est-à-dire la rationalité morale autant qu’intellectuelle dont Piaget a cherché à connaître et à expliquer la genèse, en concevant au reste celle-ci comme s’inscrivant dans le prolongement d’un autre problème fondamental qu’il s’est également employé à résoudre, à savoir celui de la genèse de formes biologiques adaptées à leur niche écologique (rappelons-nous ici les ses travaux sur l’adaptation des limnées et dont on trouve une trace dans certains ouvrages importants du 20^e siècle traitant de l’évolution des espèces). Si, donc, l’œuvre psychologique de Piaget est appelée à interpeller encore longtemps toute personne s’interrogeant sur la nature humaine, c’est que, au cœur des nombreuses recherches qu’il a réalisées ou dirigées, se trouve ce questionnement radical de notre être auquel l’essor de la pensée humaine nous a irrémédiablement entraîné.

Pour ce dernier cours, après un bref rappel des quelques territoires de l’œuvre sur lesquels nous nous sommes arrêtés plus ou moins brièvement ces semaines passées, je vais rapidement évoquer quelques travaux de psychologie complémentaires de ceux déjà exposés, travaux qui révèlent l’impact du développement de l’intelligence sur des fonctions telles que la perception, l’image mentale ou encore la mémoire, ou encore éclairent les mécanismes par lesquels sont construits ces structures intellectuelles et cognitives de plus en plus puissantes dont on a pu suivre les étapes principales dans les précédents cours.

Un rappel

Lors des précédents cours, nous avons commencé par prendre connaissances du contexte intellectuel à partir duquel l’œuvre a pris son envol, et notamment du rôle déterminant joué par la double formation en biologie et en philosophie, puis en psychologie de l’enfant et en philosophie des sciences. Dans un second temps, nous avons vu que, bien que Piaget, dans son œuvre psychologique, se soit avant tout intéressé aux questions qui touchent à la genèse de l’intelligence et des catégories de l’esprit (le temps, l’espace, les quantités logico-mathématiques ou physiques), il a également consacré un effort assez conséquent à résoudre le problème des rapports entre l’intelligence et l’affectivité, ainsi que le problème de la genèse du jugement moral, en montrant que si l’affectivité est un élément moteur de toutes les conduites humaines (leur « essence », l’ « énergie » qu’elles exigent), l’intelligence, au sens le plus large, est ce qui permet de rendre compte de leur structure (de leur « mécanique »), et des jugements de valeur qu’elles impliquent plus ou moins explicitement en ce qui concerne leurs objets, leurs visées et leurs résultats. Enfin, dans un troisième temps, nous avons parcouru à grands traits (en limitant le nombre de domaines examinés) les grandes étapes et leurs sous-étapes par lesquelles passent la genèse de l’intelligence sensori-motrice puis représentative avant d’aboutir, finalement, lors de l’enfance puis de l’adolescence, à des structures de pensée concrètes puis formelles, qui sont à la fois instruments d’adaptation au monde réel, constitutives de la raison humaine et sources des sciences logico-mathématiques et physiques.

En guise de résumé du parcours accompli ces dernières semaines, nous allons découvrir quelques travaux complémentaires réalisés par Piaget et ses collaborateurs. Je commencerai en rapportant quelques résultats importants d’études interdisciplinaires conduites au CIEG ayant pour objet, dans les années 1960, la genèse de la causalité physique. Ensuite, je rapporterai à grands traits des résultats de recherches qui révèlent comment le développement de l’intelligence rejaillit sur le développement de la perception, de l’image mentale et de la mémoire chez l’enfant, qui toutes trois sont, en un certain sens, la « matière » de l’intelligence en tant que celle-ci porte sur la réalité présente, passée, future ou simplement imaginée. Enfin, je donnerai un aperçu des travaux réalisés au CIEG dans les années 1970 qui, pour une large part, ont porté non plus sur les stades de développement de l’intelligence, mais sur les mécanismes de construction des structures cognitives dont il a été question dans les précédents cours.

Le développement de la causalité physique chez l’enfant

Jusqu’ici, concernant l’impact du développement de l’intelligence logico-mathématique sur la pensée physique, nous avons vu, à travers l’exemple de la conservation des liquides, comment ce développement se traduit par la construction des conservations physiques. Ces dernières jouent un rôle considérable dans la pensée physique. Si la réalité telle que nous la percevons et la concevons ne donnait pas prise à des jugements de conservation tels que ceux de la quantité de matière (par exemple, de liquide, ou de pâte à modeler), ou de poids ou encore de volume à travers les modifications de forme imprimées à cette matière, nous ne pourrions en donner aucune explication rationnelle, puisqu’elle que se réduirait alors à une sorte de chaos, de magma kaléidoscopique et informe, sans que l’on puisse y trouver aucune permanence suffisamment durable pour donner prise à la raison, y compris cette permanence des objets que le bébé, lors de ses interactions avec le réel, leur reconnaît progressivement en les faisant apparaître comme tels. C’est parce que nous pouvons concevoir et reconnaître la permanence des objets, et à partir de là des conservations de (quantité de) matière, de poids, de volume, de surface, etc., que nous pouvons appliquer notre raison logico-mathématique au monde extérieur. Mais c’est inversement parce que le réel a des propriétés de stabilité suffisante que nous-mêmes, en tant qu’objet parmi les autres, pouvons exister en tant qu’organisme puis en tant que sujet, et que nous pouvons donc construire ces instruments de pensée logico-mathématiques que sont la logique des classes, la logique des relations et l’arithmétique, instruments qui nous servent communément, à partir de 6-7 ans, à organiser et à penser concrètement ce réel. Mais la pensée physique, et même dès le développement de l’intelligence sensori-motrice, notre rapport au monde physique (dont nous reconnaissons en faire partie en tant que nous nous percevons comme objet de ce monde), ne se limitent pas à cette nécessité de découvrir et d’introduire de l’ordre dans le monde d’abord proche, puis de plus en plus éloigné dans l’espace et dans le temps. Comme nous l’avons vu en étudiant la genèse de l’intelligence sensori-motrice, c’est très tôt que l’enfant paraît « concevoir » des rapports de causalité entre lui et l’objet de ses actions, puis entre les objets eux-mêmes, conçus comme des centres autonomes d’action, distincts de l’action propre. La catégorie de causalité semble donc bien être, à la base, une catégorie innée, mais qui va profondément se transformer et se différencier au cours du développement, comme les expériences conduites par Piaget dans les années 1920 puis dans les années 1960 vont le montrer.

Que devient donc la causalité lors des étapes ultérieures du développement de l’intelligence, au delà de ses premières transformations dont nous avons suivi l’enchaînement lors de la période sensori-motrice de ce développement ? On a déjà eu l’occasion de s’apercevoir que jusque vers 4-5 ans environ, la causalité prêtée aux choses extérieures conserve des attributs empruntés à l’action propre, donc qu’elle ne se différencie pas encore de cette causalité par efficace qui se nourrit du sentiment de puissance, de force que nous éprouvons lorsque nous agissons sur le monde extérieur, mais aussi de la résistance des objets que nous ressentons et leur prêtons alors parfois. Or, pour la physique moderne, cette forme de causalité n’apporte aucune lumière sur les transformations des phénomènes physiques. Face aux abus des physiciens du passé qui étaient portés à attribuer à la réalité matérielle des forces assimilées à ce sentiment d’efficace, un courant important de la physique moderne (le positivisme) a eu la tentation d’abandonner la catégorie de causalité, et à ne plus concevoir le réel qu’en termes de lois physiques, sans chercher à apporter des explications aux régularités observées. Piaget appartient à ce lot de penseurs qui ont résisté à un tel abandon. Pour comprendre comment une catégorie différenciée de causalité physique peut amener à une explication du réel qui n’emprunte plus au sentiment d’efficace son pouvoir explicatif tout en conservant le sentiment de nécessité sans lequel il ne saurait y avoir de jugement de causalité, c’est à nouveau vers l’étude de la genèse de la causalité qu’il oriente les recherches du CIEG, une fois éclairée la genèse de l’intelligence logico-mathématique.

La solution à laquelle Piaget aboutit et qui est confortée par l’examen épistémologique des théories explicatives du monde physique élaborées par les plus grands physiciens du XXe siècle —dont la plupart n’ont pas suivi le précepte positiviste bannissant l’usage de la notion de causalité physique— est la suivante. Débarrassée de tout lien avec le sentiment d’efficace éprouvé par le sujet, la causalité physique, consiste non seulement à appliquer l’appareil logico-mathématique au réel dans le but de le mesurer et d’y découvrir des régularités et donc des lois empiriques, mais également à attribuer à la réalité physique concernée, et en un certain sens reconnaître en son sein, des structures suffisamment isomorphes aux structures propres à la pensée logico-mathématique du sujet pour que celui-ci puissent en déduire les régularités observées et par là justifier la nécessité prêtée à l’enchaînement des phénomènes physiques. Ce lien par lequel Piaget associe la causalité physique débarrassée du sentiment d’efficace avec l’intelligence opératoire est ce qui le conduit à qualifier d’ « opératoire » cette forme rationnelle de causalité qui agit au sein de la pensée physique parvenue à maturité.

Avant de donner un exemple de recherche illustrant le passage d’explications causales encore entachée d’anthropomorphisme à la seule forme acceptable —car dépsychologisée— de causalité physique, à savoir la causalité opératoire, ajoutons encore une remarque qui donne tout son sens à la solution apportée par Piaget au problème de l’origine et de la valeur cognitive de la notion de causalité physique. Les structures que le sujet en arrive à attribuer à la réalité physique ne concernent pas seulement des phénomènes dans lesquels on peut reconnaître l’effet d’actions physiques similaires, dans leur structure, aux opérations aux moyens desquelles le sujet organise et transforme la réalité physique commune qui l’entoure et dont l’exemple que nous allons tout de suite exposer livrera une illustration. Les phénomènes que la causalité opératoire éclaire peuvent être également de type purement probabiliste, comme c’est le cas dans des branches de la physique comme la thermodynamique ou la mécanique quantique, mais souvent aussi en biologie et même en sciences sociales et psychologiques, dès qu’il est question de statistique. Les structures opératoires qui sont en pareil cas attribuées à la réalité concernée peuvent être alors isomorphes à celles qui sont l’objet de la mathématique des probabilités. On trouvera sur cette question de la causalité statistique considérée comme cas particulier de la causalité opératoire une présentation très éclairante dans le deuxième volume de la monumentale Introduction à l’épistémologie physique, qui porte sur la pensée physique et dont toute une section est consacrée à l’examen de la causalité à l’œuvre en mécanique quantique [1]. Si je mentionne ici cette forme particulière de causalité opératoire, c’est uniquement pour souligner comment toute forme de référence à la causalité par efficace qui est au point de départ de la genèse de la causalité physique peut complètement disparaître des formes les plus avancées de l’explication rationnelle. On trouve d’ailleurs déjà, dans l’étude de Piaget et Inhelder sur la genèse de la notion de hasard, chez des sujets confrontés à des problèmes de mélange physique ou à des jeux de hasard tel que le tirage au sort, des indications qui vont dans ce sens [2]. Imaginons par exemple la situation suivante. Alors que, jusqu’à 9-10 ans, un enfant auquel on poserait la question de savoir pourquoi cela n’est pas toujours le 6 qui sort dans le jeu de lancer des dés ne saurait fournir d’explication convaincante, un sujet qui aura atteint le niveau de la pensée formelle pourra trouver dans sa maîtrise de la pensée combinatoire et de la notion de hasard la seule explication rationnelle qu’il convient de donner à ces suites non prévisibles de chiffres qui se succèdent les uns aux autres dans ce jeu (pour autant que le ou les dés ne soient pas pipés) : pour chaque jet de dé, il y a 1 chance sur 6 pour que le 6 sorte. Plus les jetés de dés sont nombreux, moins il est probable qu’une suite interrompue de 6 soit constatée (et il est même possible de calculer l’accroissement constant de cette improbabilité).

Mais laissons-là cette question particulière de la causalité statistique, et venons-en donc à l’examen d’une des recherches conduites au CIEG dans les années 1960 sur la causalité physique, examen qui va nous permettre de mieux comprendre la façon dont la progression des explications causales dépend de la construction des structures de la pensée opératoire. Le problème auquel est confronté les enfants de 4 à 10 ans environ est celui de la transmission du mouvement.

Un problème de transmission du mouvement

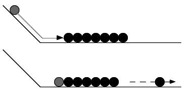
Soit la situation suivante à laquelle seront confrontés les enfants (voir figure ci-dessous) : une bille A, après avoir été lâchée sur une sorte de toboggan, vient heurter un groupe d’autres billes au repos, alignées en ligne droite sur la table, et se touchant l’une l’autre (le nombre des billes B, C, D… sur la table peut varier).

Cette situation permet d’étudier le développement de la compréhension de la transmission médiate du mouvement de la bille A à la dernière bille observée, qui seule se déplace à la suite du choc de A contre la rangée de billes alignées sur la table.

D’autres variantes de ce problème sont utilisées, dont l’une ne met en jeu qu’une bille A venant frapper une seule autre bille B. En ce cas, il y a transmission immédiate du mouvement de A à B.[3]

Dans l’expérience réalisée au CIEG, les sujets sont d’abord priés d’anticiper ce qui se arrivera lorsque la bille A sera lâchée et viendra heurter les billes au repos sur la table (ou la boule B dans le cas de la variante mentionnée ci-dessus, qui permet d’étudier les étapes de compréhension de la transmission immédiate). Ensuite, ils pourront constater ce qui se passe effectivement et ils seront alors invités à décrire ce qu’ils ont observé. Enfin, l’expérimentateur-psychologue leur demandera d’expliquer ce qui est passé. Trois étapes sont distinguées dans les réponses des enfants, la première étant elle-même subdivisée en deux sous-étapes.

Lors du sous-stade IA, présent de manière très prédominante chez les enfants de 4-5 ans, mais que l’on retrouve également chez un peu moins de la moitié des enfants de 6 ans interrogés dans cette expérience,[4] les sujets croient à une action directe de la bille A sur la dernière des billes alignées, en réduisant donc le phénomène de transmission médiate à celui d’une transmission immédiate. L’immobilité des billes intermédiaires entre la 1^ère A et la dernière, disons K, ne les perturbent pas. Rien ne les empêche en effet de concevoir, comme c’est le cas dans certaines réponses recueillies, que la bille A est passée par-dessus les autres pour venir pousser la dernière bille qui seule est partie. Pour Piaget, il est également concevable que pour certains de ces enfants, A ait même agi à distance sur la dernière bille (voir EEG 27, p. 50) [5]. En ce cas, on retrouverait à ce premier niveau, mais sur le plan de la pensée, le type de causalité magico-phénoméniste qui avait été observé dans le cadre du développement de la causalité chez le bébé (au troisième stade de la genèse de l’intelligence sensori-motrice caractérisé par l’apparition des réactions circulaires secondaires, le bébé agissait comme si un mouvement de son corps, remuer ses pieds par exemple, pouvait faire bouger un objet distant et non physiquement relié à eux).

Par contre au stade IB, qui prédomine chez l’enfant de 6 ans et même encore à 7 ans, l’explication commence à changer de nature et à se dépsychologiser, de la même façon qu’elle le devenait au 5^e stade de l’intelligence sensori-motrice. L’enfant ne croit plus à l’action à distance, du moins sur le plan des interactions physiques. Mais dès lors, comment comprendre que la bille A puisse agir sur la bille K alors qu’elle ne la pousse pas directement ? Pour ce sortir de ce paradoxe, les enfants de 6-7 ans vont majoritairement assimilé la transmission médiate à une suite de transmission immédiate du mouvement : ils affirment que les billes intermédiaires avancent chacune un peu, la première cognant la deuxième comme elle l’a elle-même été par A, puis la deuxième la troisième, la troisième, la quatrième, etc. La clé du départ de la dernière bille se trouve donc dans une certaine transitivité pseudo-empirique (c’est-à-dire imaginairement perçue et non pas déduite) accordée à la transmission du mouvement : le sujet croit voir le mouvement de A se transmettre un peu à B (poussée par A), puis un peu à C (poussée par B), etc. Comme K n’est pas suivie à son tour d’une autre bille, elle continue son mouvement. À ce niveau, la transmission reste donc assimilée à l’action propre par laquelle un sujet pousse directement sur un objet pour le déplacer, comme si chaque élément intermédiaire avait à son tour besoin de prendre de l’élan, d’acquérir de la force, pour à son tour pousser le suivant, etc.

Au stade II par contre, lequel prédomine chez les enfants entre 8 ans et 10 ans, un nouvel élément apparaît : la force physique, laquelle n’est plus assimilée au sentiment d’efficace liée à l’action propre (donc à une notion de force ou de pouvoir tout autant psychologique que physique). Pour les enfants de ce stade, l’impulsion ou l’élan pris par la bille A lors de son mouvement sur le plan incliné passe à l’intérieur de toutes les billes intermédiaires et se transmet ainsi de l’une à l’autre jusqu’à la dernière des billes qui se meut à son tour. Mais la transmission de la force de A à K implique encore pour ces enfants un léger mouvement quasi-imperceptible des billes intermédiaires, dont chacune se déplace un peu avant de revenir à sa place. Ils ne conçoivent pas encore que la force puisse passer à travers les intermédiaires sans déplacement de ceux-ci, donc de manière purement interne. La notion physique de force n’est pas encore complètement dissociée de la notion de mouvement et le sujet ne conçoit toujours pas sa conservation à travers son passage à travers les intermédiaires. La preuve en est que, pour ces enfants, la force peut varier selon le nombre d’intermédiaires, un sujet de ce stade pouvant, par exemple, concevoir que plus il y d’intermédiaire plus la force sera grande, par accumulation des forces successives que chaque intermédiaire utiliserait pour faire partir la bille suivante. Pour Piaget, l’acquisition de cette notion de force physique qui peut se transmettre de manière « semi-interne » avant que son effet final puisse devenir pleinement perceptible est la conséquence du caractère opératoire de la pensée de ces enfants, caractère qui leur fait envisager la transitivité de la transmission de la force en l’absence même de mouvements visibles. Cette conception opératoire de la transmission d’une force expliquant la transmission du mouvement ne deviendra toutefois complète que lors du troisième stade d’évolution de la compréhension du phénomène observé.

Ce troisième stade apparaît vers l’âge de 11 ans, donc avec le début de la pensée formelle. Les recherches sur le développement de la composition des forces (qui sont exposées dans le volume 30 des Études d’épistémologie génétique) révèlent que cela n’est qu’à partir de cet âge que l’on voit des sujets pouvoir composer des forces orientées dans différentes directions pour en déduire la direction et la force d’ensemble résultant de cette composition, ainsi que pleinement maîtriser le principe d’action-réaction qui explique pourquoi lorsqu’une boule A frappe une boule B identique à elle et à l’arrêt s’arrête elle-même alors que B se déplace avec la vitesse que le faisait A (si on désigne par +f la quantité de force que reçoit B de A, la réaction de B fait que celle-ci agit sur A par une force égale mais de sens contraire, à savoir –f qui annule la première [6]).

Un aperçu de cette capacité de composer les forces et leurs orientations avait déjà été observées dans la recherche sur la direction à donner à un propulseur pour qu’une bille venant frapper le bord d’un billard puisse atteindre sa cible. Que se passe-t-il donc, pour les sujets de ce niveau III, dans le cas particulièrement simple d’une bille venant heurter des billes alignées les unes à la suite des autres et qui lui sont identiques ? La transmission de l’élan (ou de la force, ou de l’impulsion) que concevaient déjà les sujets du II^e stade n’exigent plus au III^e stade le déplacement des éléments intermédiaires. La force (ou l’élan) acquise par la bille A en descendant la pente se transmet à la dernière des billes en traversant les billes intermédiaires. Si on met deux billes A et B sur le lanceur à la place d’une seule, la force totale qu’elles prennent ensemble étant double de la situation dans laquelle une seule est placée, ce sont les deux dernières billes de l’alignement qui se déplaceront à la suite du choc de A et B sur la totalité des billes au repos. Et, à revenir à la situation standard où une seule bille est placée sur le toboggan, si seule la dernière bille part à la suite de l’action de A sur l’ensemble des billes qui la précède, elle n’en agit pas moins en retour, par réaction, avec la même force que A, sur l’ensemble des billes qui la précède, le tout se traduisant par une conservation de la force acquise au départ par A en fonction de sa hauteur de chute sur le plan incliné [7].

Pour Piaget, ce qui permet aux sujets de niveau III de livrer une explication pleinement opératoire de la transmission du mouvement observée dans cette expérience est le fait que la composition (vectorielle) des forces d’action et de réaction en jeu est « liée à la constitution d’une combinatoire (pour ce qui est des directions) et de groupe de quaternalité [=groupe INRC, pour ce qui est de l’] (augmentation et diminution des actions et réactions) » (EEG, vol. 27, p. 97). En d’autres termes, les forces en jeu dans les mouvements des objets ne sont pas assimilables au sentiment d’efficace attaché aux actions propres et à la résistance que le sujet ressent lorsqu’il agit sur un objet. Il ne s’agit plus à ce troisième stade d’une assimilation des actions des objets à l’action propre du sujet sur les objets, donc d’une attribution psychologisante de l’expérience vécue aux objets, mais d’une assimilation des transmissions de mouvements et des compositions de forces aux opérations du sujet, en d’autres termes de la reconnaissance implicite que les compositions (non observables) de force expliquant les transmissions de mouvement des objets obéissent à des lois de structures au moins partiellement isomorphes aux lois qui président au fonctionnement de la pensée opératoire. D’où la formule de Piaget selon laquelle la causalité physique n’est plus, à ce stade, qu’« une attribution [bien sûr inconsciente] aux objets d’actions et d’opérations isomorphes à celles du sujet » (EEG, vol, 27, p. 97), et non pas seulement de l’application de ces dernières à la réalité physique (voir aussi EEG, vol. 26, p. 32). Notons enfin que ce lien étroit que Piaget établit entre le développement de l’intelligence opératoire et celui de la causalité physique n’est pas à sens unique. Le besoin de comprendre le réel, d’intégrer des constats qui vont à l’encontre des explications d’un certain niveau est un des moteurs principaux de la construction de la pensée opératoire (comme il l’était d’ailleurs, ainsi qu’on la constaté, de la pensée formelle) : « c’est à l’occasion d’événements ou de phénomènes à expliquer et de buts à atteindre par agencement causal que les opérations [logico-mathématiques] seront le plus exercées » (EEG 26, p. 26).

Le développement des fonctions figuratives chez l’enfant

(1) Le développement de la perception

On ne peut imaginer le fonctionnement de l’intelligence sans l’intervention des matériaux sensoriels et perceptifs directs ou indirects (c’est-à-dire de leur reproduction sous forme d’images mentales plus ou moins vivides). Le « poids » de ces matériaux ainsi que l’insuffisante prise en considération de l’activité du sujet dans la vie mentale explique le rôle qui a été attribué aux sensations, aux perceptions ou à leur prolongement sous formes d’images mentales par deux des courants les plus importants de l’histoire de la psychologie au XIX^e et au XX^ème siècles : l’associationnisme, puis la Gestaltpsychologie, la « psychologie de la forme ». Le premier a pratiquement identifié l’intelligence au mécanisme par lequel les sensations, les perceptions et leurs traces sous forme d’images (y compris d’images verbales) s’associent les unes aux autres pour former des complexes sensoriels plus ou moins durables selon le caractère répété de leur coprésence dans le champ perceptif, et peut-être aussi selon leur utilité biologique ou le plaisir lui aussi sensoriel induit par cette coprésence. Toute la psychologie de l’intelligence de Piaget se dressera contre cette conception associationniste de l’intelligence, laquelle fait du sujet un être complètement passif ou presque, en lui opposant la thèse d’un sujet agissant sur le monde extérieur, le transformant, mais aussi composant activement son paysage perceptif et mental (par exemple en orientant et en coordonnant ses perceptions, comme on va le voir dans un instant).

Quant au deuxième grand courant, la Gestaltpsychologie, il s’est lui aussi opposé —et ceci dès la fin du xix^e siècle— à la conception associationniste, non pas en mettant en lumière le rôle déterminant du sujet, mais en montrant par d’ingénieuses expériences comment les formes d’ensemble que prennent les contenus de notre champ de vision, de notre champ d’audition, etc., loin d’être le résultat de lois d’association, s’imposent à ces contenus en raison de lois de bonnes formes innées (par exemple loi de symétrie ou encore d’équilibre entre parties, etc.). Or l’une des raisons pour lesquelles Piaget, avec l’aide de ses collaborateurs, dont Marc Lambercier, consacrera plusieurs années à étudier les « mécanismes perceptifs » tient certainement au fait que les théoriciens de la Gestaltpsychologie ont tenté d’éclairer le fonctionnement de l’intelligence en le réduisant aux mêmes lois de bonnes formes supposément innées, ce qui revenait également à nier ou du moins à sous-estimer grandement le rôle déterminant des activités du sujet dans la genèse de l’intelligence, comme à nier la thèse selon laquelle les structures de l’intelligence sensori-motrice puis représentative ne sont pas innées, mais progressivement construites par le sujet (à partir, certes, de structures plus élémentaires inscrites dans le fonctionnement des schèmes réflexes). Dès lors, on comprend la place assez centrale que Piaget donnera à ses recherches sur la perception dans son œuvre psychologique. Ses travaux sur la genèse de l’intelligence sensori-motrice puis représentative lui ayant démontré la non-innéité de leurs structures ainsi que le rôle déterminant du sujet dans leur genèse, la question se posait de savoir si la thèse gestaltiste sur le caractère à la fois général et inné des bonnes formes perceptives ne pouvait pas être mise en question et même démentie de la même façon que la thèse kantienne concernant l’innéité des formes apriori de l’espace et du temps qui sont le fondement de la géométrie euclidienne et de la physique newtonienne l’avait été par les recherches piagétiennes sur la genèse de l’intelligence sensori-motrice puis représentative chez l’enfant.

Pour aborder cet examen de l’éventuelle genèse des bonnes formes perceptives observées chez les adultes par les gestaltistes et qui avait permis à ceux-ci de contredire la thèse associationniste, il était nécessaire de compléter leurs recherches expérimentales en examinant si ces formes se retrouvent chez des enfants de différents âges confrontés à des situations similaires à celles utilisées dans les travaux sur la perception chez l’adulte. Les nombreuses recherches que Piaget a lancées pour résoudre ce problème de l’innéité ou de la non-innéité des structures perceptives ont porté sur les phénomènes d’illusions perceptives ainsi que sur les constances perceptives (un objet est jugé conserver sa grandeur, alors même que sa grandeur apparente varie lorsqu’on l’éloigne ou le rapproche du sujet qui le perçoit). Donnons (en le simplifiant) un seul exemple des nombreuses recherches réalisées par Piaget et son collaborateur Marc Lambercier, à savoir l’étude de l’illusion dite de Müller-Lyer. Lorsqu’on regarde la figure suivante, qui est composée de deux segments de droite contigüs :

on perçoit le second segment comme étant plus long que le premier, alors que les deux sont égaux. Ce fait s’explique par le nombre plus élevé de micro-centrations inconscientes de notre regard sur le segment de gauche induit par le champ plus étendu offert par les diagonales qui l’encadrent (d’autres expériences confirment cet effet majeur de ces centrations ou « activités perceptives primaires », comme les désignent Piaget). Or l’étude psychogénétique de cette illusion montre que celle-ci diminue avec l’âge. La raison en est que le sujet en grandissant augmente son activité d’exploration en la dirigeant de plus en plus activement et en contrebalançant en conséquence l’effet de ces centrations primaires par des décentrations liées à cette activité exploratrice orientée. Cette activité exploratrice qui devient plus efficiente en fonction de l’âge du sujet se manifeste également lorsque la même épreuve d’estimation perceptive des longueurs est répétée plusieurs fois pendant une même séance d’expérimentation. Alors que l’illusion ne varie que très peu chez des enfants de 5-6 ans, elle diminue de plus en plus chez des sujets de 7-8 ans, puis de 9-10 ans pour se réduire encore davantage chez l’adulte. Cette expérience, confirmée par bien d’autres, révèlent donc que s’ils existent bien des illusions perceptives primaires (donc innées) dues à l’effet des micro-centrations inconscientes et à des lois de champ voisines de celles détectées par la Gestaltpsychologie, ces illusions varient en fonction de l’expérience et des activités perceptives secondaires de centration, qui elles dépendent de la genèse de l’intelligence et de la connaissance. Chacun peut d’ailleurs se convaincre de l’effet de la connaissances et des mécanismes découverts par Piaget sur la modification des illusions perceptives primaires, ainsi que l’illustrent les deux exemples suivants.

Premier exemple, qui concerne l’illusion Müller-Lyer : sachant que cette illusion est due à des centrations primaires majoritaires sur la partie de la figure dans laquelle se trouve le segment de gauche, il suffit de se forcer à regarder le segment de droite pour voir fortement diminuer et peut-être même annuler l’effet des centrations primaires.

Deuxième exemple, l’illusion du cube de Necker : lorsqu’on porte son regard sur un cube tridimensionnel représenté avec toute ses arrêtes visibles sur un plan, on voit apparaître un cube, mais celui-ci peut-être vu tantôt sous un certain angle, tantôt sous un autre, selon que les centrations primaires se portent sur telle ou telle partie de la figure).

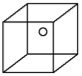Si on laisse son regard flotter sur la figure ci-jointe, on voit apparaître le cercle parfois sur la surface supérieure du cube, et parfois sur la face avant de celui-ci.

Mais là aussi, en dirigeant volontairement le regard vers tel ou tel sous-ensemble de traits (ou encore en jouant avec le clignement des yeux), il est possible de voir surgir plus ou moins durablement telle ou telle surface comme étant la partie supérieure ou la partie inférieure du cube ainsi représenté (mais sans que l’on puisse pourtant éliminer complètement les effets incontrôlés des centrations primaires) :

À noter qu’à la différence de l’illusion Müller-Lyer, d’autres illusions perceptives peuvent apparaître et se renforcer au cours même de la psychogenèse ! Le mécanisme de base reste le même : une centration perceptive tend à produire une surestimation de l’élément centré. Mais il suffit que les regards soient activement orientés de façon à se centrer et à mettre en relation des éléments du champ perceptif non reliés l’un à l’autre, ou à accumuler volontairement les explorations visuelles d’une figure vers telle ou telle de ses parties pour que telle ou telle illusion s’accroisse ou mieux que se forment ce que Piaget appelle alors des « illusions secondaires »[8].

Ce rapide résumé [9] permet ainsi non seulement de concevoir comment le développement de l’intelligence peut agir sur les mécanismes perceptifs, mais également de saisir l’apport spécifique de Piaget par rapport aux deux grands courants de l’associationnisme et de la Gestaltpsychologie. Du premier, il retient le rôle important que joue l’expérience et sa répétition dans les transformations de la perception. Mais il s’accorde également avec le second en montrant que tout dans la perception ne se réduit pas à une simple addition de sensations d’abord isolées pour être ensuite progressivement associées les unes avec les autres. Des formes ou même des déformations apparaissent d’emblée qui ne résultent pas de la simple association liée à la coprésence d’éléments perçus dans un même champ perceptif, mais s’expliquent par des mécanismes internes à l’appareil sensoriel du sujet (centration perceptive avec effet déformant, exploration et sélection active de partie du champ perceptif, décentration et régulation perceptive permettant de compenser les effets des centrations primaires, etc.). Mais ce que découvre Piaget va au-delà des satisfecits partiels attribués à l’un et à l’autre de ces deux courants. D’une part il insiste sur le rôle actif que joue le sujet dès le départ, de manière très généralement involontaire et même inconsciente, de par la capacité qu’il a de moduler ses centrations du regard, leur succession, de les sélectionner en fonction de l’expérience acquise, etc., ce qui conduit à diminuer les déformations, les augmenter ou les neutraliser). Enfin, dernière originalité des recherches piagétiennes sur l’évolution des formes et des mécanismes perceptifs : la comparaison entre certaines structures perceptives (par exemple la constance de la grandeur d’un objet, quel que soit l’éloignement de cet objet) et les structures propres à l’intelligence (le groupement des déplacements, ou encore les regroupements des opérations logiques, arithmétiques, et géométriques) permet de mettre en évidence une différence essentielle qui a échappé aux théoriciens de la Gestalt lorsqu’ils ont assimilé la résolution intelligente de problèmes tels que ceux auxquels Kœhler a confronté les chimpanzés à l’apparition des bonnes formes perceptives. Dans le cas de la perception, c’est un processus largement inconscient d’équilibre statistique entre centrations qui conduit à atténuer les effets déformants des centrations primaires. Au contraire, pour ce qui est de l’intelligence sensori-motrice, il y a, chez le sujet, conscience des relations en jeu dans la résolution des problèmes pratiques (comme on l’a vu au 5^e et surtout au 6^e stade du développement de cette première forme d’intelligence) ; et, pour ce qui est de l’intelligence représentative concrète puis formelle, conscience des rapports entre opérations directes, inverses et/ou réciproques qui seule permet au sujet de conclure avec nécessité logique à la présence de telle ou telle propriété (par exemple la conservation), une nécessité absente des constances perceptives qui, elles, ne sont toujours qu’approximatives.

(2) Le développement des images mentales

Avant de présenter l’essentiel des résultats des recherches piagétiennes sur le développement de l’image mentale dans ses rapports avec le développement de la pensée opératoire, rappelons-nous que le problème de la genèse de l’image mentale a déjà été abordé dans le contexte des travaux de Piaget sur la naissance de l’intelligence chez le bébé. En fait cette question de l’origine de l’image mentale dérive directement de la formation de la pensée biologique de Piaget, dans les années 1910. Le biologiste F. le Dantec, après avoir défini dans les années 1890, la vie élémentaire (celle des organismes unicellulaires) comme un processus d’assimilation des substances chimiques externes à la « substance vivante » de chaque organisme, en était arrivé à concevoir qu’au niveau de l’évolution des formes de vie pluricellulaires, l’adaptation des espèces à leur milieu, supposée expliquer la genèse des espèces, pouvait être identifiée à un processus d’accommodation au milieu, lui-même conçu comme un mécanisme d’imitation, se prolongeant ensuite sur le plan de la genèse des connaissances. Lorsque, à la suite de la naissance de ses enfants, c’est-à-dire dès 1925, Piaget s’est lancé dans l’examen de la genèse de l’intelligence, tout en rejetant le primat accordé à l’accommodation sur l’assimilation, il a repris non pas le détail de la thèse de le Dantec à laquelle il s’opposait d’ailleurs, mais l’importance accordée aux processus conjoints d’assimilation et d’accommodation dans l’explication de l’évolution, ainsi que l’existence d’un certain lien entre le processus d’accommodation et le processus d’imitation. Cet emprunt initial à ce qui n’était encore, pour l’essentiel, que pure spéculation chez le Dantec était par ailleurs enrichi par la connaissance qu’au début des années 1920 Piaget avait prise des travaux et des thèses du psychologue J.-M. Baldwin, lequel, trouvant probablement son inspiration chez le philosophe H. Spencer, avait lui aussi accordé une place importante aux notions d’accommodation et d’imitation dans ses travaux pionniers, mais encore largement spéculatifs, sur le développement de l’intelligence chez l’enfant et dans l’espèce humaine. En d’autres termes, Piaget n’a pas créé ab ovo le cadre notionnel qui va orienter ses travaux sur le développement sensori-moteur du bébé dans ses deux premières années de vie postnatales, mais il a profondément modifié et enrichi le sens de ces notions (assimilation, accommodation, intelligence et imitation) grâce à la manière systématique dont il a recueilli, classé et examiné les très nombreuses conduites presque journellement observées (avec l’aide de sa femme) chez ses enfants, dont, en particulier, ce qui de loin ou de près s’apparente à de l’imitation (comme par exemple le phénomène de contagion des pleurs, observé dans les semaines qui suivent la naissance, qui n’est pas encore une véritable imitation psychologique). C’est ainsi qu’il est parvenu à retracer les étapes de développement de l’imitation qui, pour lui et comme le suggérait le Dantec, prend sa source dans la fonction accommodatrice inhérente à l’adaptation organique. Et c’est ainsi également qu’il a été conduit à découvrir que, dans sa dernière étape de développement sensori-moteur, l’imitation donne naissance à l’image mentale, celle-ci n’étant rien d’autres, à la base du moins et à la lumière de cette filiation, qu’une conduite d’imitation intériorisée et différée (c’est-à-dire se réalisant en l’absence même de la chose imitée, et avec pleine conscience d’imiter) [10].

Pour en terminer avec ces considérations préliminaires, notons encore que l’un des résultats principaux de ces premiers travaux sur la genèse de l’imitation psychologique a été de reconnaître que l’image mentale est avant tout, comme la perception, non pas une copie passive de l’objet (Piaget doute même qu’il y ait jamais copie passive), mais, à la base du moins, une copie active, l’image mentale pouvant bien sûr ultérieurement se détacher de cette fonction imitatrice, pour se faire créatrice, par exemple dans le contexte de la formation des jeux symboliques, dans lesquels c’est non plus la fonction accommodatrice qui prime, mais la fonction assimilatrice, le réel ou les images se ployant au bon plaisir du sujet.

Cela dit, venons-en maintenant à la question des liens entre le développement ultérieur de l’image mentale et le développement de l’intelligence opératoire [11]. De multiples recherches et situations expérimentales ont été mises en place dans les années 1950 et au début des années 1960 pour étudier ce rapport. Là encore, je ne présenterai, en la résumant, qu’une seule de ces recherches, ce qui suffira à illustrer comment le développement de l’intelligence agit sur la capacité d’imaginer de l’enfant. Avant de la présenter, disons un mot sur la méthode. L’image mentale ne pouvant être directement observée, elle l’a été indirectement, en demandant par exemple aux sujets de reproduire ou d’anticiper par le geste ou par le dessin une situation qu’on leur présentait visuellement ou qu’un leur décrivait. Comme on va le voir à travers la recherche en question, cette manière de procéder a été fructueuse. Les situations qu’il s’agissait de reproduire par un dessin ou, pour certaines, par un geste étaient soit de type statique et cinétique, (par exemple une tige posée sur une grande feuille, dont on demande de la dessiner plus loin sur cette grande feuille, ou bien encore de la dessiner après une simple translation, ou après une rotation), soit de type transformatrice (par exemple, dessiner la transformation d’un arc de cercle en droite, avec ou sans les étapes intermédiaires de cette transformation, ou encore le dessin de la rotation d’une tige, même si elle ne concerne pas une transformation physique [12]). Cantonnons-nous à l’une des situations les plus simples, dans laquelle l’expérimentateur-psychologue montre rapidement à des sujets de 4 à 9 ans le mouvement de rotation de 90° d’une tige fixée à un pivot, avant de leur demander de représenter les deux positions extrêmes de la tige, ainsi qu’une ou quelques positions intermédiaires. Trois procédés de représentation sont utilisés par chacun des sujets : le dessin, l’imitation par un geste (l’enfant doit reproduire par geste, au moyen de la tige, différentes moments du mouvement de rotation préalablement perçu) et enfin le choix, parmi des dessins faits d’avance, de celui qui paraît représenter le mieux les différentes étapes du mouvement de la tige [13]. Voilà les résultats recueillis par Inhelder et l’un de ses collaborateurs.

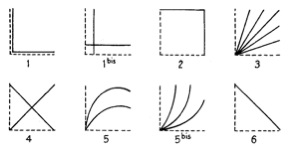
Commençons par présenter les types inadéquats de dessins, de produits de geste d’imitation, ou d’images réalisés ou choisies par les sujets pour représenter le mouvement de rotation de 90° rapidement présenté au préalable (voir figures ci-dessous).

Fig. 1
(Traité de psychologie expérimentale, vol. 7, p. 86)

Quant au tableau résumant l’évolution des proportions (en %) des réponses des enfants entre 4 et 9 ans il est le suivant (5% des enfants de 4-5 ans n’ont pas livrés de dessins) :

	Dessins corrects	Dessins incorrects	Choix corrects	Imitations correctes
4-5 ans (18 sujets)	23%	72%	21	7%
6 ans (17 sujets)	47%	53%	46	43%
7 ans (17 sujets)	65%	35%	81	87%
8-9 ans (11 sujets)	82%	18%	82	82%

Bien qu’à prendre avec prudence (il est clair que les techniques actuelles d’imagerie cérébrale permettraient de formuler des interprétations plus certaines), la progression des proportions laisse supposer que les enfants font appel à leur maitrise progressive, de plus en plus forte à partir de 6-7 ans, des opérations spatiales pour se représenter ou anticiper les positions intermédiaires prises par la tige au cours de sa rotation (le développement de ces opérations a été étudié au moyen de différentes situations dans le cadre des recherches sur la représentation spatiale chez l’enfant, recherches dont il a été question à la fin du 6^ème cours).

La mémoire et le développement de l’intelligence opératoire

Comme la perception et l’image mentale, la mémoire des activités, des objets, des personnes ou encore des situations et des événements passés est la troisième des grandes fonctions psychologiques susceptible de livrer à l’intelligence la matière de son activité organisatrice, transformatrice et explicatrice. Cette mémoire du passé, laquelle est faite de souvenir et que Piaget et Inhelder qualifient de « mémoire au sens strict », doit être distinguée de la mémoire au sens large, laquelle inclut la « simple » conservation des schèmes d’action et de représentation [14]. La mémoire au sens strict se laisse elle-même subdiviser en deux : 1° la mémoire de recognition (non pas simplement reconnaître tel objet, telle action ou telle situation : par exemple son biberon, l’action de taper, l’ouverture d’un porte, mais aussi —conduite plus avancée— se souvenir, lors de la perception d’une action, d’un objet, d’un événement ou d’une situation, de l’avoir déjà perçu dans le passé, en le rapportant plus ou moins clairement, et en tant que précédemment saisi, à ce même objet ou à cette même situation, ou bien encore à un objet ou une situation similaire), et 2° la mémoire d’évocation (se souvenir d’un événement passé non revécu dans la situation actuelle, sinon à travers ce souvenir). À partir de leurs multiples études antérieures sur la psychogenèse des fonctions cognitives, ainsi probablement que par leur connaissance des thèses de Pierre Janet sur la nature et l’évolution de la mémoire, Piaget et Inhelder admettaient certainement d’emblée que, comme l’image et la perception, la mémoire au sens strict est avant tout affaire d’activité et de construction et non pas simplement de conservation, ce qui ne veut pas dire que celle-ci n’en soit pas une condition sine qua non, bien au contraire puisque, comme toute activité psychologique, cette forme de mémoire repose sur l’activation de schèmes déjà acquis d’action, de perception ou de pensée. Et c’est bien parce que le mécanisme de conservation des schèmes intervient dans le contexte de fonctionnement de la mémoire au sens strict que les auteurs auraient pu, sans autre impulsion, concevoir un plan de recherche basé sur l’hypothèse que le développement de l’intelligence, et en particulier de l’intelligence opératoire doit conditionner le développement de la mémoire (au sens strict), et plus particulièrement la construction du souvenir, de la même façon qu’elle conditionne le développement de la perception et de l’image mentale.

Dans les faits toutefois, ce n’est pas cette hypothèse, aussi évidente qu’elle eût pu paraître à leurs yeux, qui a sans autre conduit les deux auteurs à initier une recherche sur les rapports entre Mémoire et intelligence (titre d’un important ouvrage publié en 1968). Il vaut la peine de conter ici la façon dont Piaget et Inhelder sont arrivés à mettre en place tout un ensemble d’épreuves permettant d’étudier systématiquement ce rapport, dans la mesure où elle illustre l’esprit tout à la fois dialectique et clinique (au sens de la méthode clinique-critique inventée par Piaget) dans lesquels la psychologie génétique piagétienne a progressé d’une étape à l’autre de ses recherches.

Dans l’avant-propos qu’ils cosignent avec leur collaboratrice Hermine Sinclair [15], Piaget et Inhelder rapportent les faits suivants. Lors des recherches sur l’image mentale, il avait déjà été constaté que lorsque les enfants étaient confrontés à un problème de transformation opératoire (par exemple de transvasement de liquide) ou un problème de « configuration sériale » (par exemple une sorte d’escalier construit avec des plots) et qu’ils étaient réinterrogés quelques heures ou quelques jours après dans le but de tester une hypothèse sur le rôle de l’activité du sujet dans la formation des images, le souvenir qu’il conservait de la configuration-modèle ou du résultat d’une transformation (dans l’exemple du transvasement des liquides), dépendait de son niveau de développement opératoire, mais aussi du fait que le sujet était invité ou non à opérer (par exemple à reproduire au moyen de cubes la configuration-modèle). Ce résultat n’avait rien d’étonnant à leurs yeux, puisqu’il ne faisait qu’apporter une confirmation à ce qui avait maintes fois été observé dans les recherches sur le développement de l’intelligence opératoire : si le niveau de développement opératoire d’un enfant rejaillit sur l’interprétation voire la perception que les sujets se font des configurations d’état résultant d’un processus de transformation ou servant de modèle à une activité de sériation, il faut s’attendre à ce que le souvenir soit d’autant meilleur lorsque les sujets auront été invités non seulement à percevoir (ce qui implique aussi l’activation d’un schème d’assimilation), mais aussi à agir. Mais ce qui a peut-être surtout décidé les auteurs à mettre en place toute une série d’enquêtes psychogénétiques sur les rapports entre mémoire (au sens strict) et intelligence, c’est la découverte faite par l’un d’entre eux [16] se retrouvant par hasard face à un enfant qui avait déjà été interrogé six mois auparavant sur le même problème qu’il (ou elle) s’apprêtait à lui poser. Dans cette heureuse circonstance, l’expérimentateur-psychologue eut l’idée de lui demander s’il pouvait raconter « s’il se souvenait de la présentation antérieure » (Mémoire et intelligence,p. vi). Or ce qu’il y eut de tout à fait remarquable dans sa réponse, c’est que le souvenir de cette présentation était supérieur à la reproduction qu’il en avait donnée une semaine après. En d’autres termes, alors que l’on s’attend communément à ce que tout souvenir ne fasse que se détériorer ou tout au plus se conserver au cours du temps, dans ce cas précis, qui concernait vraisemblablement l’image-souvenir d’une configuration sériale, le souvenir s’était transformé de manière à reproduire non pas ce que l’enfant avait perçu, fait ou affirmé six mois auparavant, mais ce qu’il aurait perçu, fait et affirmé si son niveau de développement opératoire avait été supérieur au niveau auquel il se trouvait alors ! Le caractère spectaculaire et inattendu de ce fait alors isolé n’a pu que pousser les auteurs à lancer une recherche systématiquement conduite sur les rapports entre la mémoire et l’intelligence.

Cette recherche a conduit à deux résultats importants. D’une part elle a permis de confirmer que le souvenir peut progresser en fonction des niveaux de développement de l’intelligence opératoire (comme l’illustrera une des enquêtes psychogénétiques que je vais tout de suite présenter et qui porte précisément sur le souvenir d’une sériation non plus de plots formant une sorte d’escalier mais de baguettes de plus en plus grandes). Mais d’autre part elle a également révélé que les étapes intermédiaires du développement opératoire —étapes riches en contradictions cognitives dues à des schèmes d’interprétation entrant en conflit les uns avec les autres [17]— peuvent se traduire par des déformations du souvenir « destinées à lever un conflit » (op. cit., p. vi).

Examinons maintenant de plus près le lien étroit qui existe entre la mémoire et l’intelligence, en l’illustrant au moyen de la première des expériences présentées dans l’ouvrage de 1968, laquelle prolonge très directement les recherches sur l’image mentale chez l’enfant.

La mémoire d’une configuration sériale simple de baguettes

On se rappelle les étapes franchies par les enfants lorsque, après leur avoir montré une sériation achevée de baguettes, on leur demande de reproduire la même chose, le même « escalier » qu’on vient de leur montrer. Au 1^er stade, ils posaient des couples ou des trios de baguettes ; au 2^e stade, ils parvenaient à construire de manière empirique, par tâtonnement un telle sériation, et enfin au 3^e stade, ils inventaient un schème opératoire à partir de leur connaissance de la notion opératoire et transitive de la relation de grandeur (un élément intermédiaire d’une sériation est à la fois plus petit (ou plus grand) que les éléments auxquels il succède, et plus grand (ou plus petit) que les éléments qu’il précède. [18] Étant entendu que la sériation qui sert de modèle est une « bonne forme perceptive », en d’autres termes qu’un jeune enfant la reconnaît sans difficulté en tant que forme globale, la question se pose de savoir ce qui se passe quelques jours, semaines ou mois après que les sujets aient été interrogés.

Or, comme on l’a déjà laissé indiqué ci-dessus, lors de l’une des recherches entreprises sur le développement de l’image mentale chez l’enfant, Piaget et Inhelder avaient déjà constaté le fait suivant : demander au sujet, lors d’une 1^ère séance, de reproduire effectivement, et non pas seulement de percevoir, une configuration sériale de plots formant un escalier et présentée comme modèle, se traduisait, lors d’une deuxième séance d’expérimentation programmée 1 ou 2 semaines après la première, par un dessin reproduisant un peu mieux le modèle perçu lors de la 1^ère séance. Plus précisément, ce résultat démontrait déjà que l’activité du sujet (soit la mise en œuvre, lors de la 1^ère séance, d’une activité effective chez les plus jeunes, et non pas seulement d’une perception attentive du modèle ou même d’ailleurs de l’activité de l’adulte construisant ce modèle) favorise une reproduction comparativement meilleure par rapport par rapport à des sujets qui, lors de la première séance, n’ont pas eu l’occasion d’agir (mais ont dû se contenter de percevoir le modèle ou de percevoir l’adulte construisant la configuration). Cependant la question de fond posée dans la nouvelle étude sur les rapports entre mémoire et intelligence ira au-delà de la seule question de savoir si la mise en œuvre de schèmes d’action et non pas seulement de perception facilite ou non la construction d’un souvenir. Il s’agissait avant tout par cette étude d’examiner les effets du développement de l’intelligence opératoire sur l’évolution des souvenirs, et en ce qui concerne le cas particulier de la mémoire d’une configuration sériale, d’examiner si le développement du schème de la sériation mis en évidence dans les recherches sur le genèse de l’opération de sériation transforme le souvenir, ainsi que le suggérait le cas de cet enfant retrouvé par hasard et dont le souvenir était plus exact après 6 mois qu’après 1 semaine.

Voilà un résumé incomplet de la procédure utilisée pour mettre à l’épreuve cette supposition dans le contexte d’une simple configuration sériale de baguettes de différentes grandeurs. Dans une première séance, l’expérimentateur-psychologue demande aux enfants de bien regarder « pour pouvoir s’en rappeler » la série toute faite composée d’une dizaine de baguettes de grandeur régulièrement croissante. Dans une deuxième séance, qui a lieu une semaine plus tard, les sujets doivent reproduire par le geste, puis par un dessin ce qu’ils ont perçu la première fois. Si les enfants ne parviennent pas à reproduire un dessin correct, on leur montre à nouveau le modèle, comme lors de la première séance, et on leur demande de le copier pour connaître leur niveau exact de reproduction en présence du modèle. En dernière partie de cette deuxième séance, l’expérimentateur teste également leur niveau de développement à l’épreuve classique de la sériation [19], et ils leur demandent de décrire verbalement les éléments de la série afin de mesurer leur niveau de langage dans l’utilisation des expressions de grandeur telles que « grand », « petit », « plus grand », « plus petit », etc. [20] Enfin vient la troisième séance, entre 6 à 8 mois plus tard, au cours de laquelle l’expérimentateur demande aux enfants de dessiner la série de baguettes perçue qui leur avait été présentée plusieurs mois auparavant.

Avant d’examiner la question de l’évolution après 6-8 mois du souvenir de la configuration sériale, commentons brièvement les différents types de réponses données par les enfants aussi bien lors de recherches antérieures sur le développement de la sériation, que dans le groupe de sujets qui, lors de la deuxième séance de cette nouvelle recherche, faute de livrer un dessin correct, ont été priés de dessiner la série de baguettes qu’on plaçait alors à nouveau devant eux :

Mémoire et intelligence, p. 39

Les types I à II E correspondent à trois sous-étapes du premier stade de développement de la conduite de sériation des longueurs chez l’enfant. Le type III de dessin correspond au stade intermédaire de la conduite de sériation (l’enfant réussit à construire par tâtonnement une série de baguettes de plus en plus grandes). Enfin le même dessin se retrouve chez les enfants de niveau opératoire (un enfant qui sait sérier opératoirement des baguettes n’a évidemment aucune difficulté à reproduire par le dessin la série de baguettes qui lui a été montrée auparavant : il est plus facile de dessiner les lignes les unes à côté des autres que sélectionner opératoirement des baguettes bien réelles de différentes grandeurs pour les sérier).

Voilà les résultats principaux auxquels a conduit cette recherche. En ce qui concerne les résultats de la deuxième séance, il confirme ce qui avait déjà été constaté dans le cadre de la recherche sur le développement de l’image mentale : l’existence d’ « une correspondance assez générale entre le niveau opératoire de chaque sujet et l’organisation de son souvenir après une semaine » (Mémoire et intelligence, p. 46). En effet, les enfants de niveau franchement préopératoire (début du stade I) dessinent presque tous une série de type I (voir la figure précédente) lorsqu’ils sont invités à reproduire ce qu’ils ont vu une semaine auparavant (un seul produit un dessin de type II). Il en va en général de même pour les enfants qui sont soit au stade intermédiaire (construction par tâtonnement d’une sériation), soit au stade opératoire (utilisation répétée du schème opératoire du « plus grand des restants ») : tous ou presque parviennent à livrer un dessin tout à fait exact (donc de type III=IV) de la série de baguettes qu’ils avaient pu percevoir une semaine auparavant (les quelques exceptions concernent des enfants de niveau intermédiaire, qui dessinent une série de type II C, II D ou II E). Par contre un certain nombre des enfants qui sont à un niveau plus avancé du stade préopératoire (leur sériation aboutisse à des configurations identiques aux types II B-C-D-E), parviennent à fournir un dessin légèrement plus avancé que leur sériation effective, et même 1/3 d’entre eux (soit 7 sur 35, le plus souvent de niveau II C-D-E) parviennent à dessiner une sériation de niveau III, alors même qu’ils ne parviennent pas à sérier par tâtonnement une dizaine de baguettes. Il n’y a en ce cas pas de correspondance totale entre le niveau opératoire de ces enfants et le niveau de leur dessin, celui-ci étant un peu plus en avance que la capacité de sérier effectivement des baguettes. Pour Piaget et Inhelder, l’explication la plus plausible de cette avance du dessin réside dans le fait que pour dessiner une telle série, il n’est nul besoin de choisir entre des baguettes préexistante ; il suffit de tracer les uns après les autres des traits de plus en plus grands. Mais la réussite observée chez ces enfants ne signifie pas qu’ils copient un souvenir exact de la série de baguettes qui aurait été conservé en mémoire après en avoir vu le modèle lors de la première séance. Je reviendrai dans un instant sur ce point, mais ce qu’il est important d’avoir déjà à l’esprit, c’est que cette réussite peut être due non pas à la conservation pure et entière d’un tel souvenir, mais au fait que le sujet utilise pour construire son dessin un schème d’action correspondant à son niveau de développement (pré)opératoire de la conduite de sériation (soit le schème de tracer des traits de plus en plus grands, lequel n’implique pas que le sujet ait déjà acquis le schème de sériation opératoire des longueurs !).

Mais venons-en maintenant à l’examen des dessins recueillis lors de la troisième séance, soit quelques 6 à 8 mois après la première, chez un petit groupe de sujets que les psychologues ont pu retrouver et inclure dans la dernière étape de cette recherche (au final, 24 sur 120, dont peut-être l’enfant qui, par un heureux hasard, a reconnu les adultes qui l’avaient interrogé au début de leur recherche et auxquels il a décrit le souvenir qu’il avait conservé de cet ancien échange).

En 6-8 mois, chez ces enfants dont l’âge était presque chez tous compris entre 4 et 6 ans, le schème de sériation des longueurs ne pouvait que progresser (sauf bien sûr chez les plus avancés d’entre eux qui étaient déjà au niveau opératoire lorsqu’ils ont été testés lors de la deuxième séance). La question qui se posait alors et à laquelle cette troisième phase de l’expérience devait apporter des éléments de réponse était de savoir dans quelle mesure cette progression s’est répercutée sur leur reproduction par le dessin de la série perçue lors de la première séance.

Ce qui était demandé aux enfants lors de la troisième séance, était d’abord de dessiner ce qu’on leur avait montré 7-8 mois auparavant, puis de donner une description verbale de la série des baguettes qui leur était alors à nouveau présentée. Or le résultat a été probant : sur les 24 dessins des dessins recueillis, 22 manifestaient une légère avance par rapport aux dessins que leurs auteurs avaient réalisés lors de la deuxième séance, avance correspondant à celle connue de la progression du schématisme opératoire, par exemple le passage de II C à II E, ou même à III (voir plus haut, les étapes de cette progression). En d’autres termes, le souvenir que chacun de ces 22 enfants avaient, à travers leur dessin, de la série qui leur avait été présentée quelques mois auparavant était supérieur au souvenir qu’ils s’en faisaient 1 ou 2 semaines après. La question qui se pose alors est de savoir quelle est la cause de cette transformation majorante du souvenir, question qui soulève celle de la nature même de ce dernier.

La progression du souvenir constatée dans cette expérience comme dans les autres exposées dans Mémoire et intelligence semble contredire la conception classique d’un souvenir-pur, passivement conservé dans une sorte de réservoir stockant plus ou moins durablement les perceptions passées de chaque individu, souvenir qui serait restitué de manière plus ou moins intacte ou dégradée lors de son rappel. Au contraire, cette progression corrobore l’hypothèse selon laquelle le souvenir que le sujet se fait de l’événement passé est largement déterminé par le niveau de développement du schème de sériation. Néanmoins, un problème subsiste. Ne peut-on pas expliquer l’exactitude plus grande du dessin livré après 6-8 mois par le fait que le sujet, lors de chaque acte intermédiaire de remémoration, aurait le sentiment que son dessin ne correspond pas complètement à la perception originale ? Et l’hypothèse classique d’un réservoir stockant plus ou moins durablement les perceptions passées de chaque individu ne reste-t-elle dès lors pas une condition de l’explication recherchée ?

Piaget et Inhelder n’ignorent pas qu’un tel sentiment puisse jouer un rôle. Seulement, même en considérant ce facteur, il n’est nullement nécessaire, selon eux, d’évoquer la présence d’un souvenir pur conservé dans une mémoire-réservoir (et ne pouvant que se dégrader avec le temps). Ce qui intervient lors de la deuxième séance comme lors de la troisième, ce n’est pas seulement la mémoire d’évocation, reconstruisant au moyen du dessin ce qui a été précédemment perçu, mais également la mémoire de recognition, qui, elle, est toujours le fait d’un schème d’assimilation perceptive (lui-même inclus dans le même complexe de schèmes activés lors de chaque séance). Lorsque le sujet qui n’a pas encore atteint le niveau III ou IV de réalisation du dessin (niveau lui-même dépendant du développement de sa capacité de sériation) est confronté au dessin qu’il vient de tracer et qu’il a sous les yeux, la situation est suffisamment similaire à celle vécue une semaine ou quelques mois avant pour que, si un sentiment d’insatisfaction se produit, celui-ci découle du fait que le schème de perception alors activé n’aboutit pas à une recognition suffisamment en accord avec ce à quoi tout schème « s’attend » lorsqu’il se saisit de son objet. Mais ce qui peut se produire en effet chez quelques sujets n’apparaît pas nécessairement chez tous les autres. Il se peut en effet tout à fait —et c’est là l’hypothèse que Piaget et Inhelder privilégient— que ce qui seul entre en scène lors de la 3^e séance soit le schème d’action de refaire ce qui a été réalisé précédemment, ce qui a été fait lors de la deuxième séance dépendant lui-même d’un schème d’action dans lequel était impliquée la capacité plus ou moins développée de tracer des traits petits et grands, voire de plus en plus grands, et donc de sérier, activité qui elle-même était préparée dès la 1^ère séance, puisque l’expérimentateur-psychologue annonçait à l’enfant qu’il devait regarder attentivement le modèle qu’il avait sous les yeux et qu’il aura à reproduire plus tard. Or comme par ailleurs l’activité générale de comparaison des grandeurs et donc de sériation progresse dans toute sorte de contextes, cette progression générale ne peut que se répercuter sur la qualité du dessin, de telle sorte que, lorsque 8 mois après le sujet dessine une sériation qui correspond exactement à la sériation perçue initialement, cela peut être un by-product de cette seule progression du schème de sériation préopératoire (schème qui, encore une fois et dans sa forme la plus générale, s’exerce dans bien d’autres circonstances que celui de sérier des baguettes).

Les mécanismes centraux de construction des structures cognitives:
l’équilibration majorante et l’abstraction réfléchissante

Nous nous rapprochons du terme de ce cours. Avant de donner un jeter un dernier regard sur l’ensemble de l’œuvre, il reste à présenter brièvement une des parties les plus importantes de la psychologie et de l’épistémologie de Piaget : à savoir sa conception des mécanismes de construction cognitive.

Ainsi que l’on a pu le constater aujourd’hui et dans les précédents cours, c’est la quasi-totalité du développement psychologique, et non pas seulement intellectuel et cognitif de l’enfant, qui dépend très largement du développement d’abord de l’intelligence sensori-motrice, avec les structures de regroupement d’actions qui la caractérise, puis de l’intelligence représentative, dont l’essor est rythmé par la genèse des structures opératoires, d’abord concrètes, puis formelles. La théorie qui découle des nombreuses recherches psychogénétiques réalisées par Piaget et ses collaborateurs est l’une des rares, sinon la seule [21], qui parviennent à livrer une explication d’ensemble de la quasi-totalité de la vie mentale, au moins dans les 15 premières années qui suivent la naissance. Cela ne signifie pas que cette explication soit complète, loin de là, car d’autres facteurs explicatifs interviennent qui seuls peuvent rendre compte de la trajectoire de vie, toujours singulière et originale de chaque individu (l’un devenant jardinier ou mathématicien, l’autre maçon ou physicien), ou encore des différences plus ou moins grandes que l’on peut constater dans le développement cognitif de sujets appartenant à des cultures et sociétés différentes [22]. Mais cela signifie que les caractéristiques les plus universelles que l’on peut découvrir chez l’humain sont toutes ou presque rendues un peu plus compréhensibles aujourd’hui qu’elles ne l’étaient au début du 20^e siècle. Reste une grande question à laquelle Piaget a consacré une grande partie de sa dernière décennie de recherches : comment se construisent ces structures qui jalonnent et constituent le noyau de l’intelligence et de la raison humaines ?

Si l’on jette un regard d’ensemble sur le développement de l’intelligence tel qu’il ressort des nombreuses enquêtes psychogénétiques piagétiennes, deux grands processus ou mécanismes paraissent s’imposer tout naturellement : l’abstraction réfléchissante et logico-mathématique, et l’équilibration majorante. L’abstraction réfléchissante tout d’abord, qui, à la différence de l’abstraction empirique ou physique porte non pas sur la réalité intéroceptive ou extéroceptive pour en extraire des régularités ou des formes de plus en plus générales, mais sur les coordinations préexistantes propres aux « actions ou opérations du sujet », en réfléchissant et reconstruisant sur un plan supérieur (par exemple celui propre aux opérations combinatoires) « ce qui est tiré d’un niveau inférieur d’activité » [23] (dans cet exemple, celui des opérations concrètes).

1. L’abstraction réfléchissante

Elle dérive immédiatement de ce constat que, à chaque grande étape de leur développement, l’intelligence et la connaissance semblent se faire tout à la fois de plus en plus abstraites (comme lorsque l’on passe de l’intelligence sensori-motrice à la pensée opératoire concrète, puis de celle-ci à la pensée formelle), et de plus en plus riches et puissantes, par le nombre de plus en plus élevé de schèmes d’actions et d’opérations qui les composent, ainsi que par la multiplicité et l’étendue de plus en plus grandes des objets sur lesquelles elles portent, ceci sans que soient perdues les conquêtes intellectuelles et cognitives précédemment acquises (pour autant qu’elles soient suffisamment stables et fonctionnelles). Après que Piaget a découvert que l’intelligence sensori-motrice et la construction du réel correspondant s’expliquent par des regroupements de schèmes d’action obéissant à des lois de structure, puis que la raison concrète (le premier « âge de raison ») qui se manifeste chez l’enfant entre 6 et 9-10 ans s’explique elle aussi par la présence sous-jacente de structures opératoires, et qu’enfin la pensée de l’adolescent répond elle aussi à des lois de structures, en revenant sur ces trois découvertes successives et en les comparant, l’hypothèse ne pouvait que s’imposer avec la plus grande force selon laquelle chacune des deux dernières étapes de construction de l’intelligence et de la raison humaines étaient construites à partir de structures préalablement acquises à l’étape précédente (hypothèse d’autant plus forte que c’était le même constat qui pouvait être parallèlement fait sur le terrain de l’histoire des sciences, par exemple lors du passage de la géométrie euclidienne aux géométries posteuclidiennes, ou encore de la physique de Newton à la théorie de la relativité, ou encore de l’algèbre classique à la théorie des groupes, etc., constat qui, lui, n’était pas seulement le fait de Piaget, mais également celui de philosophes des sciences tels que Gaston Bachelard). Seulement un tel constat établi parallèlement sur le terrain de la psychogenèse et de l’histoire des sciences, s’il imposait l’hypothèse d’un mécanisme d’abstraction par lequel la pensée de l’enfant puis des savants pouvaient passer d’un moindre niveau à un niveau plus élevé d’abstraction logico-mathématique, restait lui-même par trop « abstrait », cette fois au sens le plus usuel de ce terme, dans la mesure où le processus d’abstraction par lequel le sujet est supposé procéder d’un palier à un autre de la construction des structures restait largement inconnu dans le détail de son mécanisme. Pour un savant tel que Piaget, habitué depuis son adolescence non seulement à appuyer ses hypothèses sur des faits, mais à les enrichir à partir de leur examen, une telle hypothèse, aussi convaincante soit-elle, ne pouvait pleinement le satisfaire. Il lui fallait comprendre comment ce mécanisme agit effectivement chez le sujet et c’est certainement ce manque de connaissance qui l’a incité à lancer des recherches empiriques sur cette abstraction réfléchissante par laquelle, comme l’avaient révélé les travaux sur la genèse de l’intelligence sensori-motrice, puis de l’intelligence opératoire concrète puis formelle, d’anciennes structures acquises sont réfléchies et reconstruites sur un nouveau palier de développement.

Il n’est pas possible ici d’entrer dans le détail de ces recherches. Disons seulement un mot de la démarche expérimentale utilisée et des résultats principaux auxquels elle a conduit. La méthode est la suivante : confronter les enfants à des problèmes dont la résolution implique la maîtrise d’opérations d’opérations « logico-arithmétiques » ou « géométriques », et, en plus d’observer les actions des sujets interrogés, leur demander comment ils comptent s’y prendre pour obtenir le résultat souhaité, ou d’anticiper le résultat d’une action, ou encore, à différentes étapes de leur essai de résolution, leur demander de décrire et de justifier la façon dont ils se sont pris pour avancer dans la résolution recherchée, ou, pour finir, et s’ils y sont parvenus, pour atteindre la solution. Ce faisant, l’expérimentateur-psychologue amène chaque sujet à réfléchir, dans la mesure de ses capacités, sur l’activité qu’il vient de produire ou qu’il va entreprendre, ou aux raisons qui l’ont poussé à formuler tel ou tel jugement. Illustrons cette démarche par un seul exemple de recherche, réalisée par Alina Szeminska [24] et qui concerne l’usage d’opérations arithmétiques élémentaires dans la situation suivante (très lacunairement résumée).

Soit deux réserves d’éléments composées, l’une, de plots bleus et l’autre de plots rouges. Dans chaque réserve, les plots sont de deux tailles, l’une, petite (disons 1) l’autre grande (soit n fois plus grand qu’un petit, avec n pouvant varier de 2 à 5, selon les situations). L’une des réserves est attribuée à l’enfant interrogé, l’autre à l’expérimentateur. Enfant et expérimentateur commencent par extraire un à un et simultanément le même nombre de plots qui leur serviront ensuite à construire deux murs, parallèles l’un à l’autre de manière à pouvoir comparer leur longueur. Selon les situations, les plots extraits par les deux protagonistes seront de même taille (tous des grands ou tous des petits), ou de taille contraire (par ex., tous des grands pour l’enfant et tous des petits pour l’adulte). Lors de chaque nouvelle situation, un premier mur sera construit en alignant les uns après les autres des plots extraits de l’une des deux réserves de départ, puis le deuxième mur le sera de la même façon, mais en utilisant les plots extraits de la seconde réserve. Enfin, avant la construction du second mur, l’enfant sera invité à prévoir si, une fois construits, les deux murs auront ou non la même longueur. D’autres questions ou problèmes sont en outre posés aux enfants, dont nous verrons un exemple dans la suite. Examinons maintenant les résultats principaux de cette recherche.

Dans les cas où enfant et expérimentateur ont pris un à un et simultanément des plots de même grandeur, l’anticipation du résultat final est évidemment beaucoup plus facile. Dès lors, les enfants de niveau préopératoire pourront, dès 4-5 ans, admettre que le deuxième mur sera la même chose long du simple fait que « les plots sont les mêmes » (= de même taille ; cf. p. 12) ; mais ces mêmes enfants pourront au contraire, après une telle première correcte anticipation, refuser de se prononcer si on leur demande ce qui se passerait en continuant de construire exactement de la même façon les deux murs ; pour eux, pour le savoir, il faudrait effectuer cette construction, ce qui permettrait alors de voir si les deux murs ont ou non toujours la même longueur. Ces deux types de réponse corroborent (et sont confirmés par) toute une série de recherches qui montrent que le processus d’abstraction logico-mathématique (et d’ailleurs plus généralement de prise de conscience de l’action propre) tend à se porter sur les résultats d’une action (en l’occurrence l’égalité constatée des deux longueurs de murs) avant que ne soit considérées les actions les produisant (addition successive d’un même nombre de briques de taille égale).

À une sous-étape un peu plus avancée du niveau préopératoire, les enfants pourront utiliser non seulement l’argument selon lequel les plots sont égaux, mais également le fait que les plots pris pour faire le mur l’ont été en même temps (correspondance terme à terme entre actions), les uns, dans le tas des rouges, les autres dans le tas des bleus. Par contre, dans les cas où expérimentateur et enfant décident d’avance de prendre un à un et simultanément, l’un, des petits plots dans sa réserve, et l’autre, des grands plots, la question d’anticiper où arrivera le deuxième mur —question à laquelle les enfants de 4-6 ans échoueront— amènera les enfants plus avancés à réfléchir sur les actions en jeu. Si par exemple chaque plot bleu est 2 fois plus grand qu’un plot rouge de grandeur égale à 1, et si l’expérimentateur a placé, disons, 5 plots rouges, les enfants qui, vers 7-8 ans, maîtrisent les opérations additives pourront, en réfléchissant sur les actions réalisées, additionner le même nombre de fois la différence de 1 qui existe entre 2 et 1, et donc prévoir que le mur des plots bleus sera de 1+1+1+1+1 = 5 (plots-rouges) plus long que le mur de plots rouge — ou même, s’ils sont encore plus avancés, utiliser, vers 9-10 ans, la maîtrise de la multiplication arithmétique pour en déduire que le mur bleu sera 5×1=5 (plots-rouges) de plus que le mur rouge. Mais le problème deviendra encore plus complexe, et sa résolution encore plus tardive, si, une fois les deux murs construits et leur différence de longueur reconnue (dans l’exemple cette différence est de 5 fois plus grande), le sujet est invité à prévoir de combien sera la différence si l’on ajoute un même nombre, par exemple 4, de grands plots au mur bleu et de petits plots au mur rouge. En ce cas, la solution exacte, qui ne sera atteinte vers 11-12 ans environ, exigera des sujets la maîtrise des opérations de proportionnalité, dont les recherches sur la genèse de la pensée formelle ont montré qu’elles mettent en œuvre des opérations au deuxième degré (des opérations sur des opérations).

Comme on le voit, à la différence des recherches précédemment conduites sur la construction des opérations arithmétiques élémentaires chez l’enfant, ou des opérations de proportionnalité chez l’adolescent, cette nouvelle recherche sur l’usage des opérations arithmétiques, ainsi d’ailleurs que toutes celles exposées dans les volumes 34 et 35 des Etudes d’épistémologie génétique, n’ont plus pour objet la mise en évidence des grandes étapes de construction de ces opérations logico-mathématiques dont nous ne cessons de faire usage dans notre activité de tous les jours. C’est bien maintenant le ou les processus d’abstraction qui est ou sont visé(s) par Piaget et ses collaborateurs à travers le comportement et les réponses des enfants confrontés à des problèmes logico-mathématiques destinés à en révéler les détails. Or, en plus de montrer très concrètement comment les sujets de différents âges ou niveaux de développement utilisent l’abstraction pour répondre aux problèmes qu’on leur pose et à réfléchir (ou non) les actions qu’ils viennent d’effectuer ou qu’ils s’apprêtent à entreprendre, un des résultats peut-être les plus intéressants de l’étude sur l’abstraction réfléchissante a été de montrer que le processus d’abstraction par lequel le sujet réfléchit et se représente son action se transforme et s’enrichit lui-même aux différentes étapes de son développement intellectuel.

Pour le dire très brièvement, alors qu’un enfant préopératoire ne pourra, dans le contexte de la recherche résumée ci-dessus, qu’effectuer des abstractions pseudo-empiriques portant sur les résultats des actions que lui ou l’expérimentateur ont effectuées [25] (ce qui l’amènera soit à anticiper l’égalité des murs construits avec des plots de même taille, en justifiant cette égalité par le seul constat de l’égalité des tailles, soit à refuser une telle anticipation, faute de pouvoir constater la longueur du mur non encore construit) ou tout au plus qu’esquisser un processus d’abstraction réfléchissante portant sur la correspondance entre actions et ne faisant qu’expliciter verbalement celle-ci, un enfant ayant atteint le niveau des opérations concrètes va réfléchir sur plusieurs des actions en jeu et chercher à les coordonner de manière à résoudre des problèmes inaccessibles aux enfants préopératoires, cette abstraction réfléchissante ne se limitant alors plus à de simples constats, mais se faisant également constructive. Mais à son tour le sujet ayant atteint le niveau des opérations concrètes ne va pas procéder à une abstraction réfléchissante de la même façon qu’un sujet de niveau formel le fait lorsque tous deux portent leur attention sur la suite des démarches et des actions que chacun s’apprête à entreprendre ou qu’il a effectuée, ceci dans le but de résoudre tel ou tel problème logico-mathématique. Le pouvoir de réflexion constructive et de thématisation de l’action (ou des opérations) s’accroît en proportion même du niveau d’intelligence opératoire atteint par chacun des sujets interrogés ! Ainsi le processus d’abstraction réfléchissante qui commence très tôt, car on peut déjà observer une forme élémentaire de sa mise en œuvre dans les tâtonnements du bébé confronté à des problèmes d’intelligence pratique (voir l’exemple de Jacqueline essayant de comprendre les conditions permettant de passer un bâton à l’intérieur de son parc [26]), finit au niveau supérieur de la pensée formelle par aboutir non seulement à la construction de nouvelles structures opératoires toujours plus puissantes sous-tendant les conduites intellectuelles et les connaissances du sujet, mais à intégrer dans sa réflexion les résultats même des processus antérieurs d’abstraction réfléchissante — des résultats qui reflètent eux-mêmes les opérations du sujet et qui, comparés les uns aux autres, et coordonnés les uns avec les autres et avec ces opérations, aboutissent à une connaissance de plus en plus réfléchie et explicite des structures opératoires en jeu (mais sans encore, naturellement, aboutir à ces formes de théorisation que l’on trouve dans les sciences logico-mathématiques, et qui elles-mêmes deviennent tout à la fois de plus en plus abstraites, explicites et puissantes). À revenir aux exemples que nous avons rencontré lors de notre examen de la pensée formelle, cette forme supérieure d’abstraction réfléchissante que l’on trouve chez l’adolescent peut être illustrée par ce sujet de 15 ans environ qui, confronté à un problème de combinaison chimique, parvenait à expliquer pourquoi c’est seulement en procédant selon une démarche combinatoire complète, que l’on peut être certain d’atteindre la ou les solutions recherchées à ce problème [27].

2. L’équilibration majorante

Que dire de cette notion d’équilibration sinon qu’elle est peut-être la plus ambitieuse de toute l’entreprise piagétienne. Dès le départ de son œuvre scientifique ou presque, et plus précisément dès que Piaget s’est interrogé sur l’évolution de la vie sur le triple plan des réalités biologiques, psychologiques et sociales, cette notion ou plutôt le mécanisme qu’elle vise lui sont apparus comme seuls à même de livrer une explication scientifique de cette triple réalité. Pourquoi ? Parce que tout d’abord la réalité psychologique et sociale aussi bien que la réalité biologique est affaire d’organisations, d’êtres organisés, c’est-à-dire de totalités qui, chacune à son niveau, sont indissociablement déterminées par les parties qui les composent, autant que chacune de ces parties est dépendante du tout dont elle est membre. En ce sens, Piaget est proche à la fois du philosophe Herbert Spencer qui, en plein milieu du 19^e siècle, concevait la vie comme essentiellement affaire d’organisation et d’équilibration parties-tout, mais aussi proche de cette Gestaltpsychologie, laquelle elle aussi insistait sur les interactions entre totalité et partie et sur leurs formes d’équilibre dans l’émergence et dans l’explication des formes perceptives et intellectuelles. Néanmoins, dès ses premières spéculations sur la progression des formes de vie biologique, psychologique (en particulier intellectuelle et morale) et sociale Piaget a adopté une conception qui se distançait de ces deux explications. La première, celle de Spencer, cédait trop au réductionnisme physicaliste, en assimilant sans les différencier, les formes d’équilibration propres à la vie à l’équilibration purement physique (celle qui explique qu’une balance atteint peu à peu son équilibre) ; la seconde ignorant par trop les étapes successives de tout processus évolutif ; et les deux ensembles ignoraient par trop ce qui fait la spécificité du psychologique, la présence d’une activité propre à ce niveau de réalité, lequel concerne aussi la vie sociale dans la mesure où celle-ci résulte d’interactions entre les individus et groupes d’individus qui la composent.

Toutefois, comme nous l’avons vu au début des 12 cours, la conception que se faisait alors Piaget de l’équilibration, si elle restera certes pendant plusieurs années à l’arrière-plan de ses recherches, ne pouvaient satisfaire à elles-seules l’idéal scientifique adopté par Piaget, c’est-à-dire le besoin de fonder toute thèse sur des faits scientifiquement reconnus et suffisamment convergents pour, sinon, la démontrer du moins la rendre suffisamment plausible par rapport à son objet. C’est bien la raison pour laquelle, dès qu’il se vouera à la recherche psychologique, Piaget laissera dans l’ombre pendant près de deux décennies la solution esquissée dans Recherche au problème de la triple évolution des formes biologiques, psychologiques et sociales. Mais les faits patiemment recueillis lors de ces deux décennies puis des années 1940 jusqu’aux années 1970 lui permettront de reprendre et de donner une assise scientifique à cette ancienne thèse de l’équilibration, d’abord un première fois, à la suite de la découverte des structures opératoires, puis une fois bien connue la genèse des structures et des notions opératoires, en raison des recherches conduites sur les mécanismes même par lesquels ces structures et notions passent d’une forme de moindre équilibre à une forme d’équilibre supérieur (d’où le néologisme « majorant » précisant le caractère spécifique de l’équilibration bio-psycho-sociologique par rapport aux processus d’équilibration physique). Pour conclure cet examen de la notion d’ « équilibration majorante », considérons donc brièvement les deux moments-clés lors desquels Piaget l’a explicitement mise en avant dans le but de rendre compte de la progression des structures opératoires. Ces deux moments se distinguent l’un de l’autre par le type d’approche ou de vision utilisée pour rendre compte du processus d’équilibration par lequel un système cognitif peut passer d’un état de moindre équilibre à un état supérieur d’équilibre. La première approche était essentiellement probabiliste, et a conduit à la présentation d’un modèle de l’équilibration inspiré de la dite théorie des jeux d’abord développée en économie mais dont la finalité générale est de mathématiser la ou les stratégies optimales qu’un individu (animal ou humain) ou un groupe social est conduit à adopter face à une situation appelant une action de sa part. Quant à la seconde approche, elle repose sur une vision moins probabiliste que classiquement mécanique de l’objet en question, dans laquelle il s’agit de décrire les actions effectives permettant à un sujet de progresser face aux situations auxquelles il se confronte.

1. Approche probabiliste de l’équilibration cognitive. — Le premier modèle de l’équilibration a été développé et publié en 1957 dans le 2^e volume des Etudes d’épistlmologie génétique [28], c’est-à-dire dans les mêmes années où Piaget créait le Centre international d’épistémologie génétique. L’orientation probabiliste alors adoptée s’imposait pour deux raisons. D’une part, dans les années 1940, les recherches réalisées sur les mécanismes perceptifs imposaient cet usage, de par le fait que les centrations perceptives expliquant la formation des illusions perceptives répondaient, comme on l’a vu, à un mécanisme de nature essentiellement statistique. D’autre part, dans les années 1940 et 1950 la théorie des jeux, utilisant elle-même des instruments de modélisation essentiellement statistique, débordait largement le domaine de l’économie pour s’étendre à l’ensemble des sciences sociales. Comme en outre cette théorie pouvait être rapprochée de la thermodynamique, domaine où les notions d’équilibre et d’équilibration sont centrales, on comprend que Piaget et ses collègues du CIEG, dont le mathématicien Benoît Mandelbrot, ne pouvaient pas ne pas prendre appui sur cet outil de modélisation du processus permettant aux structures cognitives et plus généralement aux réponses comportementales du sujet de passer d’un état inférieur à un état supérieur d’équilibre.

On a déjà aperçu ce processus lors de notre examen de la progression des conduites des enfants confrontés à un problème tel que celui de la conservation d’un liquide lorsque celui-ci est transvasé d’un verre dans un autre de forme différente (par exemple plus allongé). C’est précisément ce genre de situations qui est au cœur de la modélisation probabiliste esquissée par Piaget en 1955-1956 ou 1956-1957. Pour aller au plus simple, voyons comme l’équilibration est alors conçue dans le cas de la conservation des liquides (dans la suite de son texte, Piaget généralise cette esquisse d’abord faite dans ce cas particulier, en appliquant la même approche probabiliste à l’explication du passage des structures préopératoires aux structures opératoires concrètes, puis de ces dernières aux structures formelles). Confronté au problème de conservation des liquides, un enfant de niveau préopératoire adoptera avec une très forte probabilité la « stratégie la plus primitive », c’est-à-dire « la moins coûteuse » en fonction de ses connaissances acquises, et qui consiste à « ne centrer que l’un des deux caractères opposés A de la nouvelle configuration » (op. cit., p. 49 et p. 56), en l’occurrence, la hauteur A du nouveau verre par opposition à sa largeur B (si le nouveau verre est de forme plus allongée, et que le niveau de l’eau s’élève en conséquence). Cette stratégie conduit donc à un jugement de non-conservation. La deuxième stratégie « consiste à centrer l’autre des deux caractères B, jusque là négligé » (p. 50). Ce déplacement de centration peut être soit involontaire (tôt ou tard, un élément centré perd son intérêt, pour une raison qui échappe au sujet), soit volontaire. Dans les deux cas, la nouvelle stratégie est un peu plus coûteuse que la première ; contrairement à ce qui se passe en perception, il faut en effet « échapper à une persévération et changer de point d’attention » (p. 56), mais dans les deux cas, le sujet passe sans difficulté d’un jugement de non-conservation (« il y a plus dans ce verre ») à un autre (« il y a plus dans cet autre verre »). La troisième stratégie (p. 51) correspond aux conduites de type intermédiaire : le sujet passe intentionnellement d’une centration à l’autre, en continuant à formuler des jugements de non-conservation, mais qui lui paraissent cependant poser problème de par leur aspect contradictoire ou incertain. Cette troisième stratégie est intellectuellement plus coûteuse que les précédentes, puisqu’elle implique de réelles mises en relation des caractères A et B en jeu (p. 57). Enfin la quatrième stratégie consiste également à mettre en relation les dimensions en jeu, mais cette fois en les coordonnant de manière compensatrice, et en intégrant le fait qu’aucune quantité de liquide n’a été ajoutée ou supprimée lors du transvasement (p. 52). Cette dernière stratégie est certes la plus coûteuse de par le nombre de coordinations réalisées par le sujet ; mais elle a le rendement le plus élevé, puisque son résultat est stable : il offre un gain de sécurité et de prévisibilité optimal (p. 57 ; le jugement de conservation ne peut pas être remis en cause, du moins tant que l’on ne sort pas de cette situation propre à la réalité communément partagée par tout être humain parvenu à ce niveau de développement cognitif [29]).

La caractéristique de ce premier modèle de l’équilibration cognitive est claire. Elle consiste, comme déjà indiqué, à rendre compte de ce mécanisme essentiellement à travers un outillage probabiliste et de calcul des coûts et des rendements qui, s’il permet de mettre en évidence l’optimisation croissante des « stratégies » du sujet, n’en tend pas moins à oblitérer ce qui se passe sur le plan de la « mécanique interne » au sujet (pour ainsi dire). L’activité du sujet est bien présente dans ce premier modèle, mais sous une forme squelettique qui la rend apte à être traduite dans le langage de la théorie des jeux. Or, en rapportant quelques exemples des recherches sur le développement de l’intelligence sensori-motrice puis de l’intelligence représentative, on a vu que tout ne se réduit pas à des questions de stratégie, de coût et de rendement. L’intelligence est composée de schèmes qui entrent en conflit les uns avec les autres ; le sujet éprouve des déséquilibres, des contradictions, auxquels il est confronté lorsqu’il s’agit de résoudre des problèmes dans lesquels il est question d’espace, de temps, de quantités physiques, logiques ou arithmétiques, etc. (par exemple, lorsqu’il s’agit de rendre compte de ce fait paradoxal d’une lune qui nous suit lorsqu’on se déplace, ou de cet autre fait que les personnes paraissent à l’envers lorsqu’on les regarde en mettant sa tête entre ses jambes, ou bien encore de partage équitable de tranches de gâteau, ou bien pour nous adultes, lorsqu’on veut comprendre pourquoi, lors du passage à l’heure d’été il s’agit d’avancer l’heure de sa montre et non pas de la retarder, ce qui au premier abord semble vouloir impliquer que la journée sera plus courte, et donc que nous pourrons moins profiter d’une longue soirée d’été, etc.). Tout l’intérêt du second modèle de l’équilibration sera de ne pas négliger cette vie intellectuelle interne du sujet lorsque celui-ci se confronte à des problèmes de coordination logico-athématique dont la complexité est proportionnelle à la capacité toujours plus grande d’intégrer les innombrables facettes d’une réalité elle-même toujours plus enrichie par les créations plus ou moins libres ou contraintes de l’intelligence représentative (le monde des idées, des possibles). Ce second modèle fait l’objet du 33^e volume des Etudes d’épistémologie génétique, publié en 1975, sous le titre L’équilibration des structures cognitives. Problème central du développement.[30]

2. L’équilibration majorante des structures cognitives. — Dans l’avant-propos de ce 33^e volume des Etudes d’épistémologie génétique, publié presque 20 ans après Logique et équilibre, Piaget caractérise lui-même comme insuffisant le modèle proposé en 1957, et de fait, le nouveau modèle entre dans la dynamique interne même de l’équilibration, par laquelle le sujet cherche constamment à dépasser les lacunes ou les limites de ces précédentes constructions de schèmes d’actions et d’opérations au moyen desquels il organise le monde et sa propre pensée, et au moyen desquels il cherche à constamment enrichir sa compréhension des choses. Trois aspects de ce processus d’équilibration sont longuement présentés dans ce nouvel ouvrage. Le premier concerne la filiation qui inscrit le cognitif dans le prolongement du biologique : la présence dans les deux cas d’une recherche d’équilibration entre les deux processus d’assimilation et d’accommodation qui interviennent constamment lors du fonctionnement de tout schème ou systèmes de schèmes interagissant avec leur objet. Le deuxième, les processus de différenciation, d’intégration (et donc d’équilibration) qui interviennent dans le cadre des relations parties-tout (ou entre des systèmes cognitifs et leurs sous-systèmes, voire même le système entier de tous les schèmes et les parties de ce système). Enfin, le troisième porte sur les processus de coordination pratiques ou inférentielles et de constatation (engendrant des observables) toujours à l’œuvre dans les interactions du sujet et de l’objet, que cet objet concerne le monde physique ou qu’il concerne les idéalités logico-mathématiques. Nous avons pu nous faire une certaine idée de l’équilibration entre les pôles assimilateurs en examinant la progression des schèmes sensori-moteurs. De même, pour le deuxième, nous nous en sommes également fait une idée en examinant le passage des opérations et des structures opératoires concrètes aux opérations et structures opératoires formelles (les secondes intégrant les premières en dépassant leurs limitations génératrices de sentiments de lacune et, donc, de déséquilibre, moteurs des nouvelles rééquilibrations majorantes). Quant au troisième, un schéma extrait de l’ouvrage de 1957 donne une certaine idée de la dynamique de construction de nouvelles coordinations débouchant sur de nouveaux instruments d’assimilation autorisant conduisant à de nouveaux observables :

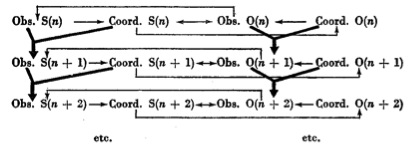
En tout comportement ou presque, le sujet porte d’abord son attention sur l’objet qui se présente à lui (Obs. 0(n)), et consciemment ou non, il est capable de saisir les coordinations propres à l’objet (et en particulier les rapports de causalité) en fonction des coordinations de ses propres actions ou opérations (Coord. S(n)) dont il est capable à ce niveau n ; selon les problèmes auxquels il se heurte, un mécanisme de prise de conscience et d’observation de ses propres caractéristiques entre en scène (Obs. S(n)) qui vont soit être intégrées au Coord. (s(n)) soit vont exiger la construction d’une système cognitif S(n+1) dépassant les limites du système S(n) composé des observables et coordinations maîtrisées de niveau (n), etc.

On notera ici que le processus d’équilibration peut se dérouler aussi bien dans des problèmes qui n’exigent pas le passage à des structures opératoires de niveau supérieur (en d’autres termes, des problèmes d’application [31] des capacités opératoires acquises, comme c’est le cas d’un adolescent maîtrisant la pensée hypothético-déductive, qui doit se familiariser avec un contexte particulier tel que celui d’un problème de combinaison des corps chimiques, et qui pour ce faire observe le résultat de ses opérations, observe ces dernières et coordonne en conséquence les opérations à entreprendre pour atteindre le but fixé, ce qui lui permet du même coup d’expliquer les faits observés), que dans des situations-problèmes qui exigent la construction progressive d’une structure opératoire de niveau supérieur (par exemple les opérations combinatoires par rapport aux opérations élémentaires de classification et de sériation).

Sans pousser plus avant l’explicitation de ce modèle, on pressent en quoi ce qu’il vise va bien au-delà du précédent modèle (puisqu’on peut l’appliquer à tous les systèmes et sous-systèmes cognitifs qui interviennent dans l’activité psychologique du sujet, depuis le sensori-moteur, jusqu’au fonctionnement de la pensée adulte, et que ces systèmes portent sur les idéalités mathématiques ou sur les réalités naturelles de toute espèce. Citons d’ailleurs ces quelques lignes de Piaget qui décrit le point principal par lequel le nouveau modèle dépasse les limites du précédent : « Dans le modèle dépassé le moteur initial consistait en probabilités de rencontre avec les caractères observables de l’objet, l’abstraction réfléchissante n’intervenant que dans la suite lors des coordinations opératoires ou de leurs ébauches quasi opératoires. Dans le présent modèle, au contraire, il y a dès le départ interaction entre les observables et les coordinations, donc collaboration à tous les niveaux entre les abstractions empiriques et réfléchissantes, celles-ci jouant par conséquent de façon continue un rôle moteur nécessaire » (p. 63).

* * * * *

Un dernier regard

Au cours de ces quelques semaines, nous avons pris connaissance, de manière plus ou moins approfondie, des principaux domaines des recherches piagétiennes : la biologie, la philosophie, la logique, l’épistémologie et bien sûr la psychologie du développement et en particulier du développement cognitif, objet central de ce cours. À survoler ces domaines comme nous l’avons fait, à effleurer des chapitres d’histoire de la philosophie et des sciences, nous ne pouvons être que stupéfaits devant l’ampleur de l’œuvre, son originalité, son indéniable apport aux sciences auxquelles Piaget a consacré l’essentiel de son effort de recherche, mais aussi la profondeur de son enracinement dans des contextes intellectuels qui ont marqué l’évolution des sciences et des idées au 19^e siècle et au 20^e siècles. De nombreux savants et philosophes des sciences du siècle passé nous impressionnent bien sûr également par l’ampleur de leur œuvre. Mais je crois bien qu’aucun autre penseur n’est parvenu à créer et à développer une nouvelle discipline scientifique capable de rendre autant raison de la raison que Piaget y est parvenu avec l’épistémologie génétique et son lien indissociable avec la biologie, la psychologie génétique, l’histoire et l’épistémologie (ou philosophie) des sciences, la sociologie et la modélisation logico-mathématique. Il reste cependant quelques mots à dire concernant les domaines ou les activités que l’on n’a pas pu aborder, et qui sont cependant étroitement associés à ces champs d’étude privilégiés, notamment les domaine de l’enseignement et, plus généralement, de l’éducation.

Les travaux et les thèses développées par Piaget en psychologie et en épistémologie génétiques ont eu un large écho dans le courant de ce que l’on appelle l’école active, c’est-à-dire une forme d’éducation dans laquelle l’activité du sujet, ainsi que l’importance de développer l’autonomie intellectuelle et morale de l’enfant, sont goût d’apprendre et de faire œuvre d’originalité dans le développement des idées priment sur la façon plus répandue de concevoir l’éducation avant tout comme une inculcation aux élèves du savoir acquis au cours des générations de penseurs et de savants. Ce n’est pas que Piaget négligeait cette composante de l’éducation. Il avait bien conscience que ce qu’un enfant apprend aujourd’hui dépend largement de l’apport des générations passées. Mais ce que souhaitait Piaget, c’est que pour toute connaissance qui s’y prête, l’éducation favorise une réelle activité de reconstruction par les élèves des savoirs préalablement découverts ou formulés par les savants et les moralistes du passé. Toute connaissance ou presque exige, pour être vraiment assimilée et donc comprise, que le sujet se la soit appropriée grâce à cette activité reconstructrice qui fait usage des mécanismes constructifs tels que l’équilibration et la majoration dont on vient de voir un aperçu. Il est cependant vrai que, par l’intérêt qu’il portait, dans ses recherches, à l’individu en tant que tels (hormis dans ses travaux où il étudiait par exemple l’évolution du jeu de règles chez les enfants), Piaget a par la force des choses (c’est-à-dire pour des raisons principalement méthodologiques : impossibilité de remonter au passé de l’espèce et de la préhistoire pour recueillir toutes les informations qui devraient l’être pour comprendre la genèse de la raison humain à travers les générations d’individus) valorisé avant tout ce qui relève de cette activité spontanée qui est sans cesse au cœur de sa conception du développement cognitif (et moral). Il est vrai, en conséquence que s’il admet le rôle joué par la transmission générationnelle des connaissances, mais aussi d’ailleurs par la transmission héréditaire de certains bagages cognitifs acquis par notre très lointains ancêtres, lors de la phylogenèse de notre espèce, il n’a pas analysé de près comment ces deux types d’apport indispensables (la transmission sociale et la transmission biologique) interagissent avec la construction des connaissances chez l’individu. Ou plutôt, il s’est cantonné à affirmer que ces deux facteurs jouent un rôle d’accélérateur ou de soutien, ou au contraire de frein dans les psychogenèses individuelles.

Le problème reste d’ailleurs encore aujourd’hui largement ouvert. Signalons cependant que Guy Cellérier a dès les années 1980 proposé de reconsidérer dans son ensemble et dans une direction « pluriconstructiviste » le problème du constructivisme piagétien en insistant sur le fait que les mécanismes de construction cognitive transcendent la frontière de l’individu [32]. À côté du mécanisme d’équilibration interne que l’on peut voir à l’œuvre lorsqu’on confronte le sujet à des problèmes impliquant un dépassement des instruments intellectuels qu’il a pu déjà construire dans son histoire passée, on peut entrevoir l’existence d’un mécanisme similaire, fonctionnant non pas à l’intérieur du sujet, mais dans la marche même des idées, sur le terrain des échanges et des transmissions sociales, voire sur le terrain de l’évolution biologique des espèces. Piaget n’ignorait certes pas la possibilité d’étendre sa conception constructiviste de l’évolution cognitive au domaine de l’histoire sociale des connaissances, mais aussi à celui de la biologie de l’évolution (voir sur ce point ses ouvrages de biologie des années 1960 et 1970, notamment Biologie et connaissance publié en 1967 [33]). Mais de telles réflexions, aussi fondamentales soient-elles, restaient en marge de ses recherches psychogénétiques, lesquelles offraient l’immense intérêt de n’être pas seulement le lieu de réflexion fortement spéculatives, mais de découvertes factuelles garantissant un certain fondement empirique au constructivisme à l’œuvre chez le sujet.

Les quelques réflexions jetées en guise de conclusion à ce cours ont pour but de signaler que, loin d’être complètement résolues, les questions de fond que Piaget se posait dès le début de la psychologie et de l’épistémologie génétique ne sont pas toutes résolues, loin de là. Il n’empêche que par les réponses qu’il leur a apportées (avec l’aide de ses nombreux collaborateurs) a fait franchir un pas considérable à leur résolution, pas qui se mesure, je crois, à celui qu’avait franchi par Kant dans sa Critique de la raison pure, en donnant au sujet la place une place déterminante dans les réponses à apporter à la question « Que pouvons-nous savoir ? ».

_____________________

[1] Ce volume et donc la section concernée sont téléchargeables sur le site de la Fondation Jean Piaget.

[2] J. Piaget et B. Inhelder, La genèse de l’idée de hasard chez l’enfant. (PUF, 1951).

[3] Dans une autre variante, les billes intermédiaires peuvent être remplacées par une barre d’acier, ou encore par un plot skotchés à la table). Une troisième variante utilise un dispositif, le « pendule de Newton », dans lequel les billes au repose sont suspendues verticalement à un support horizontal au moyen de tiges de même longueur. L’expérimentateur élève une ou plusieurs billes à une ou à chaque extrémité, laquelle ou lesquelles, une fois relâchée(s), heurte(nt) les billes laissées non déplacées (voir à l’adresse internet suivante une illustration simulant électroniquement le fonctionnement d’un tel pendule:
http://fr.wikipedia.org/wiki/Pendule_de_Newton.

[4] La statistique des réponses des 111 sujets interrogés est exposée à la page 51 du volume 27 des Études d’épistémologie génétique. Intitulé La transmission des mouvements, cet ouvrage est presque entièrement consacré à l’examen, à travers plusieurs recherches, de la compréhension de la transmission du mouvement chez des sujets âgés de 4-5 à 12-13 ans (voire 15 ans pour l’une des recherches). Ce volume fait suite au volume 26, qui a pour titre Les explications causales chez l’enfant, et dans lequel sont présentées de manière synthétique l’ensemble des enquêtes psychogénétiques (une centaine !) portant non seulement sur la transmission du mouvement, mais aussi sur la formation de la notion de force, ou encore sur la composition des forces, etc. En tout, ce seront quatre volumes des Études qui, en plus de celui portant sur La transmission du mouvement, seront publiés en 1972 et 1973 dans la série des Études d’épistémologie génétique ! Tous les résultats de ces recherches interdisciplinaires réalisées par la vingtaine de collaborateurs du CIEG confortent la thèse de Piaget sur la signification et la nature opératoire de la notion de causalité physique parvenue à maturité.

[5] On ne trouve toutefois pas dans les réponses des enfants illustrant ce premier stade de telles explications magico-phénoménistes, du moins dans le contexte de cette recherche sur la transmission médiate du mouvement. Dans les réponses des enfants de 4-5 ans exposées à son sujet, les enfants qui n’évoquent pas un déplacement imaginaire de A se contentent de dire que c’est cette bille et non les autres qui a poussé la dernière, sans donner plus de précision. Peut-être aurait-il fallu interroger des enfants de 3-4 ans pour en recueillir ? Ou peut-être de telles réponses ne sont pas présentées dans l’ouvrage dans la mesure où c’est le développement de la causalité physique qui était alors le centre des interrogations de Piaget ?

[6] Un bon exercice opératoire à qui veut se livrer à cette expérience relativement simple mais dont la réponse n’est pas immédiatement évidente pour qui ne la connaît pas d’avance est d’imaginer ce qui se passe lorsque, dans le cas d’un pendule de Newton composé de deux boules, les deux sont lâchées depuis la même hauteur et viennent se heurter l’une l’autre.

[7] On se rappelle que c’est seulement au stade de la pensée formelle que les sujets parviennent à découvrir que le seul facteur qui explique l’élan final acquis par une bille qui descend un plan incliné est la hauteur de chute. Si deux billes sont lancées sur le même plan, leur élan respectif restera le même, mais la force (ou l’élan total) qu’elles composent les deux ensembles sera double. Si ces deux billes viennent frapper une troisième à l’arrêt en bas du toboggan, une des deux billes sera stoppée, mais l’autre partira avec la troisième jusqu’au même point de chute auquel accède une seule bille lancée avec la même hauteur de chute.

[8] Piaget, Le développement des perceptions, in Traité de psychologie expérimentale, volume VI (La perception), 2^e éd., 1967, p. 18.

[9] On trouvera une présentation un peu plus détaillée des recherches de Piaget sur la perception sur la page [*] du site de la Fondation Jean Piaget

[10] À noter que ce lien initial entre l’image mentale et l’imitation, ne fait en un certain sens que prolonger le lien qui existe, selon Piaget, entre la perception et l’imitation alors entendue dans un sens non psychologique. Lorsque nous percevons un son ou un objet visuel ou tactile, notre appareil sensoriel s’accommode à ce qu’il cherche à saisir, il en suit le contours (du moins lors des perceptions tactiles et visuelles). Cependant, alors que la perception imite d’une certaine façon l’objet en s’y accommodant en sa présence, l’image mentale le fait en son absence (ou du moins, s’il est présent, en empêchant sa perception).

[11] J. Piaget et B. Inhelder, L’image mentale chez l’enfant, 1966, PUF. Dans la préface à cet ouvrage les deux auteurs précisent bien que cette recherche ne portait pas sur le développement des multiples facettes de l’image mentale chez l’enfant (par exemple l’imagination créatrice), mais seulement ce qui concerne la « représentation imagée dans ses relations avec le fonctionnement de la pensée ».

[12] Alors que la rotation de 90° d’une tige est rangée dans les images cinétiques dans l’ouvrage de 1966, elle est explicitement considérée comme une transformation dans le chapitre sur « Les images mentales » publié par Piaget et Inhelder dans le vol. VII du Traité de psychologie expérimentale de Fraisse et Piaget (1^ère éd., Paris, PUF, 1963, p. 85) : « Entre les images reproductrices cinétiques et de transformation, s’intercalent tous les intermédiaires, puisqu’un mouvement peut être considéré comme une transformation de position. Nous ne parlerons cependant de transformations qu’à partir des changements intéressant au moins l’orientation elle-même ». Peu importe cette divergence de classification entre ces deux publications, car ceci est affaire de convention et cela ne change rien aux quelques résultats examinés ici.

[13] On notera que cette situation est somme toute assez proche d’événements que les enfants peuvent observer dans leur vie courante (un balai, un jouet ou un livre dressé verticalement et qui chute, par exemple).

[14] À noter que ce que les psychologues d’aujourd’hui appellent la mémoire procédurale et la mémoire déclarative ne relève pas de ce que Piaget appelle la mémoire au sens strict, mais de la mémoire au sens large (bien que dans leur fonctionnement, elles peuvent faire appel à elle). Par contre la troisième forme de mémoire considérée par la psychologie contemporaine, à savoir la mémoire épisodique, relève de la mémoire au sens strict. Ce qui distingue celle-ci de la mémoire au sens large est la présence d’un rapport explicite à une action ou un événement passé explicitement reconnu comme tel.

[15] On doit à Hermine Sinclair, linguiste de formation, de multiples recherches sur les rapports entre le développement de l’intelligence et le développement du langage, et plus particulièrement de la syntaxe, qui démontrent comment la genèse des opérations logico-mathématiques conditionne l’apparition de certaines formes syntaxiques.

[16] Ou plutôt soit par B. Inhelder soit par l’une de ses collaboratrices (Piaget n’interrogeait plus lui-même les enfants à l’époque de ces recherches).

[17] Les auteurs mentionnent le genre de conflit que nous avons eu l’occasion de rencontrer en étudiant le développement de la conservation du nombre chez l’enfant, en l’occurrence, le conflit entre le nombre quotité, basé sur la correspondance terme à terme, et les grandeurs spatiales. Le rôle de ces conflits cognitifs a été réexaminé dans les recherches ultérieures conduites par B. Inhelder et Hermine Sinclair portant sur le développement des structures cognitives chez les enfants (cf. Inhelder, Sinclair, Bovet, Apprentissage et structures de la connaissance, PUF, 1974).

[18] Notons que la description des étapes de développement de la sériation présentées dans l’ouvrage de 1968 est plus précise et révèle plus d’étapes que la recherche originale exposée dans l’ouvrage de 1941 sur La genèse du nombre chez l’enfant. C’est qu’entre temps, d’autres recherches ont permis d’affiner et de compléter les premières observations recueillies par Piaget et Szeminska. On verra un peu plus loin une typologie de dessins de sériations qui illustre la totalité de ces étapes.

[19] Dans une recherche complémentaire, l’expérimentateur a appliqué la même démarche, à la différence près que le niveau opératoire n’a pas été testé au moyen de l’épreuve de sériation, de manière à vérifier que la passation de cette épreuve lors de la recherche de base, n’a pas joué un rôle déterminant dans la progression des souvenirs des enfants qui y ont été confrontés.

[20] Dans la thèse de doctorat qu’elle a soutenue en 1965 et publiée en 1967 sous le titre Acquisition du langage et développement de la pensée (Paris, Dunod, 1967), Hermine Sinclair a pu démontrer que l’évolution de ces expressions de grandeur est très étroitement liée au développement de l’intelligence opératoire.

[21] Rappelons que Piaget a pu et su s’appuyer, au départ de son entreprise, sur des œuvres telles que celles de J.-M. Baldwin et de Pierre Janet, qui eux aussi ne négligeaient aucune des facettes de la vie psychologique, et visaient à livrer une conception les englobant toutes.

[22] Piaget n’a cessé, tout au long de son œuvre, d’insister sur le rôle que jouent la maturation biologique et les interactions et transmissions sociales dans le développement psychologique, y compris intellectuel et cognitif, des êtres humains.

[23] Recherches sur l’abstraction réfléchissante. 1. L’abstraction des relations logico-arithmétiques, vol. 24 des Etudes d’épistémologie génétique (le volume 25 a pour objet et pour sous-titre L’abstraction de l’ordre des relations spatiales). A noter qu’Aristote et toute la psychologie du passé avaient déjà évoqué un processus d’abstraction pour rendre compte de la formation des idées. Mais l’abstraction qui était alors en vue portait sur la réalité extérieure, raison pour laquelle Piaget, la qualifiera d’empirique pour la distinguer de celle —réfléchissante et logico-mathématique— qui, selon lui, joue seule un rôle majeur dans la construction de structures opératoires toujours plus puissantes.

[24] On se rappelle qu’Alina Szeminska a été la proche collaboratrice de Piaget dans les recherches sur La genèse du nombre chez l’enfant (1941).

[25] Piaget qualifie de « pseudo-empirique » cette abstraction ne portant que sur les résultats d’une action et non pas sur cette action et sur les relations que celle-ci peut avoir avec d’autres actions (ici la correspondance terme à terme, ainsi que les opérations d’addition répétée ou de multiplication de la différence de taille). Il veut dire par là que ce sur quoi se porte l’attention de l’enfant n’est pas une propriété physique des objets, mais une propriété constatée sur l’objet (ici la longueur égale ou inégale d’un mur), mais qui est bien le produit d’une action du sujet (ou des deux sujets co-agissants).

[26] Cet exemple est résumé à la fin du 5^e cours portant sur « les débuts de l’intelligence sensori-motrice et de la construction du réel (stades 4 et 5) ».

[27] Voir p. 27 du 11^e cours.

[28] Piaget, « Logique et équilibre dans les comportements du sujet », in L. Apostel, B. Mandelbrot et J. Piaget Logique et équilibre, vol. II des Etudes d’épistémologie génétique, Paris : PUF, 1957. Le chapitre de Piaget est disponible ICI, à l’année 1957.

[29] Des notions de quantités physiques telles que celle de conservation de matière ou masse ne sont plus applicables dès que les mesures portent sur des objets se déplaçant à des vitesses se rapprochant de celle de la lumière. Elles sont remplacées par des notions englobantes telles que celle de matière-énergie : la matière devient une composante de l’énergie totale d’un système aux côtés de l’énergie cinétique ; seule l’énergie totale se conserve. Ce qui implique que plus la vitesse d’une particule se rapproche de celle de la lumière, plus sa masse ou quantité de matière diminue pour se transformer en énergie cinétique).

[30] Comme son titre le laisse entendre, le 33^e volume des Études d’épistémologie génétique est entièrement consacré à l’exposé du nouveau modèle d’équilibration. Ce volume est disponible ICI.

[31] Voir au sujet de la dialectique construction/application des structures, G. Cellérier, Structures cognitives et schèmes d’action I et II (in Archives de psychologie, 1979, pp. 87-104 et 107-12 ; textes disponibles ICI.

[32] Voir à ce sujet G. Cellérier, Le pluriconstructivisme, éléments théoriques (texte disponible ICI.

[33] Cet ouvrage, réédité en 1992, est disponible ICI.