J. Piaget et la psychologie du développement cognitif (IX)

Recherches sur la genèse du nombre (2^e partie)

[version PDF du cours n. 9]

[Vers: Cours n. 12 — Cours n. 11 — Cours n. 10 — Cours n. 8 — Cours n. 7 — Cours n. 6 — Cours n. 5 — Cours n. 4 — Cours n. 3 — Cours n. 2 — Cours n. 1]

Introduction

Lors du dernier cours nous avons pris connaissance des trois contextes intellectuels à partir desquels Piaget a mis en place ses travaux sur la genèse du nombre chez l’enfant. En examinant aujourd’hui quelques-uns de ces travaux, on verra que ceux-ci doivent beaucoup à l’approche kantienne consistant à rechercher les racines du nombre et donc de la science arithmétique chez le sujet (en tant qu’être agissant et transformant son milieu) et non pas dans l’objet (c’est-à-dire dans la réalité extérieure, que ce soit, à la manière de Platon, dans le monde des Idées, ou que ce soit dans l’expérience physique la plus commune). On verra également comment Piaget a pu s’appuyer sur les clarifi­cations et définitions livrées par les mathématiciens philosophes de la fin du 19^e siècle et du début du 20^e dans leur effort de fonder la science arithmétique, que ces mathématiciens philosophes s’inscrivent dans la filiation kantienne (comme Dedekind) ou au contraire la rejettent (comme Russell).

Mais là où Piaget se sépare de ces auteurs c’est dans le fait qu’étant lui aussi intéressé par le double problème de l’origine épistémologique et de la signification du nombre, il est le premier épistémologiste qui se tourne méthodiquement vers l’étude de la genèse du nombre chez l’enfant dans l’espoir d’y découvrir des faits susceptibles d’éclairer à la fois l’origine et la signification de ce nombre naturel qui, précédant l’avènement de la science arithmétique, a servi de base épistémologique et logique à celle-ci (base, qui comme on va le voir, trouve un écho dans les résultats auxquels sont parvenus ces mathématiciens-philosophes dont il vient d’être question).

À quelques exceptions près (dont, comme nous l’avons vu, Dedekind dans sa tentative de réponse à la question « que signifie et que vaut le nombre ? »), aucun philosophe ou mathématicien n’avait alors entrevu que l’étude des enfants puissent apporter quelques lumières à ce double problème. Et cela, encore une fois, parce qu’aucun ne pouvait imaginer qu’un enfant puisse être (re)créateur de cette notion par le biais d’un dévelop­pement cognitif au moins en partie (et pour les composantes les plus essentielles du nombre en très grande partie) autonome par rapport à ce que ses aînés et d’abord ses parents et ses enseignants pouvaient lui transmettre de ce savoir arithmétique dont nos lointains ancêtres avaient déjà connaissance.

Avec Piaget, la vision de l’enfant bascule radicalement non pas parce qu’il nie le rôle que peut jouer la transmission sociale dans le développement cognitif de l’enfant, mais parce que, en étendant la révolution kantienne au domaine de la psychogenèse, il conçoit l’importance déterminante de l’activité structurante propre à l’enfant, et en particulier des très nombreuses coordinations mentales que celui-ci réalise dans son effort d’assimiler le monde qui l’entoure, que ce soit lorsqu’il interagit spontanément et librement avec ce monde, ou que ce soit lorsqu’il tente d’appréhender le savoir transmis par autrui.

Mais si Piaget trouve dans l’étude psychogénétique de l’enfant des clés permettant d’éclairer l’origine et la signification du nombre « naturel » ayant servi de point de départ à la science arithmétique, en faisant ainsi bénéficier l’épistémologie des apports de la psychologie de l’enfant, réciproquement ce qu’il apprend ou a appris auprès des mathématiciens-philosophes (et de ses maîtres en philosophie et en épistémologie que furent Arnold Reymond et Léon Brunschvicg [1]) ne cesse de nourrir le regard non seulement de psychologue mais aussi d’épistémologiste qu’il jette sur les enfants et leurs notions de nombre, en lui permettant ainsi d’atteindre un niveau de perspicacité dans la lecture des faits jamais atteint par les psychologues qui l’ont précédé.

Après ce bref rappel de l’appui que Piaget a pu trouver auprès des mathématiciens-philosophes —mais aussi, sur le plan de la méthode, des psychologues de l’enfant qui l’ont précédé—, il est temps de prendre connaissance des principaux résultats de ses recherches sur la genèse du nombre, là aussi dans la double optique de connaître les notions successives que les enfants peuvent se faire du nombre, mais également de mieux cerner l’origine épistémologique et la signification ce nombre naturel qui est à la base de l’arithmétique.

A. La genèse du nombre chez l’enfant

La formation en épistémologie de Piaget lui a permis, dès le départ, de porter son attention sur trois problèmes : (1) le problème de l’invariance ou de la conservation du nombre cardinal d’un ensemble d’éléments, ou du nombre ordinal de chacun des éléments d’une série dénombrable d’objets ; (2) le problème du rôle de la corres­pondance terme à terme (ou de la correspondance biunivoque) entre des éléments de deux collections dans la construction du nombre cardinal et du nombre ordinal ; (3) le problème du rôle joué par l’ordination ou la sériation dans la mesure du cardinal d’un ensemble, ou inversement par la cardination dans l’attribution du nombre ordinal à un élément d’une série, en d’autres termes, le problème du lien ou de l’absence de lien entre classification (ou colligation) et sériation dans la construction et la compréhension intellectuelles des nombres ordinaux et cardinaux.

D’autres problèmes viendront s’ajouter par la suite, en lien avec de nouveaux constats issus de la recherche en psychologie génétique qui nécessiteront une révision des premières thèses développées par Piaget dans son ouvrage classique sur La genèse du nombre chez l’enfant (1^ère éd., 1941).

I. La correspondance biunivoque et
le problème de la conservation du nombre

Il est évident que nul ne peut prétendre avoir compris ce qu’est un nombre ou avoir pleinement différencié sa notion des autres notions de quantité si, par exemple, il suffit de modifier l’emplacement spatial des éléments d’une collection pour que le nombre cardinal de cette collection soit jugé modifié ! Pour étudier si la conservation du nombre est innée chez l’humain ou si au contraire chaque individu la (re)construit ou du moins l’acquiert au cours de sa psychogenèse [2], plusieurs situations-problèmes ou épreuves ont été posées aux enfants. J’en retiendrai deux, dont les résultats sont plus longuement exposés dans La genèse du nombre chez l’enfant : l’épreuve des perles et celle des œufs et des coquetiers (ou des vases et des fleurs).

L’épreuve des perles

Cette épreuve est la transposition sur le terrain des quantités discrètes de l’épreuve de la conservation des quantités de liquide utilisée dans le cadre des travaux sur la genèse des quantités physiques chez l’enfant. Dans cette dernière épreuve, des quantités égales de liquide sont versées dans deux verres A et B de forme rigoureusement identique. Une fois l’égalité reconnue par l’enfant, le contenu de A est transvasé dans un autre verre C de forme différente (par exemple un verre plus allongé) et l’on demande alors au sujet s’il y a plus, moins ou la même chose de liquide dans les deux verres A et C. Confronté à ce problème, les réponses des enfants peuvent sans trop d’incertitude être rangées dans l’une ou l’autre des trois étapes : la première de non-conservation, la deuxième couvrant des réponses dites intermédiaires, la troisième, caractérisée par des réponses clairement conservatoires.

Le remplacement du liquide par des perles permet d’ajouter la correspondance terme à terme aux caractéristiques de la situation sur lesquelles l’enfant peut se fonder pour répondre à cette question de conservation ou non de la quantité transvasée. Voilà de manière plus détaillée la technique utilisée dans cette épreuve de conservation d’une quantité de perles.

L’enfant a devant lui les deux verres A et B de forme identique. L’expérimentateur (E) verse des perles dans A jusqu’à ce qu’un certain niveau soit atteint. (E) demande à l’enfant de mettre la même chose de perles dans B. Celui-ci ayant terminé de mettre des perles dans B, (E) lui demande s’il est sûr qu’il y a la même chose ou si au contraire l’un a plus et l’autre moins. Quel que soit leur niveau de développement, les enfants interrogés n’ont bien sûr aucune peine à reconnaître l’égalité, puisque dans les deux verres les perles « arrivent au même niveau ». Une fois cette vérification effectuée, (E) verse alors le contenu de B dans un verre P plus petit et plus large, ou bien dans un verre L plus allongé, puis il demande à l’enfant s’il y a la même chose ou plus ou moins de perles dans P (ou dans L) que dans A. Mais il accompagne cette question standard par des questions complémentaires. Par exemple, il peut demander à l’enfant de juger l’égalité ou l’inégalité de deux colliers de perles que l’on pourrait faire, l’un avec les perles contenues dans un des verres, l’autre avec les perles contenues dans un autre verre. Dans le cas où cette question sur les deux colliers intervient juste après la constatation de l’égalité des niveaux de billes atteints dans deux verres de forme identique, les enfants répondront bien sûr tous qu’ils ont même longueur. Mais que se passe-t-il dans le cas où la même question est posée après que le contenu de l’un des deux verres de forme identique a été transvasé dans l’un des deux verres P ou L ?

Enfin, une autre manière de compléter la situation standard (donc le simple transvasement dans un verre de forme différente) consiste à demander à l’enfant de mettre la même chose de billes dans chacun des récipients de forme soit identique soit différente, ceci en procédant bille après bille, donc en mettant simultanément une bille dans chaque verre, puis une autre bille, puis une autre, etc., ce qui aboutit finalement à ce que les niveaux respectifs soient égaux lorsque les verres sont identiques, différents lorsqu’ils sont différents. Le fait que l’enfant ait procédé pas à pas et, donc, par correspondance terme à terme des actions de placer pas à pas les billes dans les deux verres va-t-il influencer les réponses des enfants, ce qui tendrait à renforcer la thèse innéiste concernant l’origine du nombre, en montrant que quel que soit l’âge des enfants, cette technique aurait pour effet de conclure à l’égalité numérique quelle que soit la forme des récipients ? Les résultats démontrent qu’il n’en est rien.

Résultats

A un premier stade, dans le cas de l’épreuve standard comme dans le cas (2) de la question portant sur la longueur respective des colliers et dans le cas (3) de l’utilisation de la correspondance terme à terme, les enfants nient la conservation de l’égalité des billes, ce qui implique la non-conservation de la quantité de billes transférées dans un verre de forme différente, et ce qui implique donc qu’ils n’ont pas encore acquis ou construit la notion de nombre au sens arithmétique du terme.

Pour le verre L par exemple, ils répondront en général qu’il y a maintenant plus de perles dans L que dans A, car le niveau atteint par les perles est plus élevé. Et si ensuite on leur demande ce qui se passe pour les deux colliers, l’un fait avec les perles, disons, rouges du verre A, et l’autre avec les perles vertes du verre L, ils répondront, à la manière de Roc (5 ans) que le collier vert est « plus long, parce qu’il a plus » (Genèse du nombre, p. 45).

Quant à l’utilisation apparemment facilitante du procédé de mettre en même temps une perle après l’autre dans chacun des deux verres, si les deux verres sont de forme identique, l’enfant pourra certes commencer par justifier l’égalité en répondant, à la manière de Coc (5 ans) : « parce qu’on met les deux » (expression sous-entendant que l’expérimentateur (E) et lui-même ont mis en même temps les éléments un à un dans les deux verres, mais pour peut-être immédiatement ajouter « non, parce que les deux verres sont la même chose » (id., p. 47), en portant attention non plus à la suite d’action simultanée (« on a mis en même temps »), mais à son résultat (« les verres sont la même chose » et le niveau atteint est le même), perceptivement plus prégnant et renforçant l’idée d’égalité. Une telle prégnance de la perception des formes spatiales sera confirmée aussitôt qu’il s’agira de se prononcer dans une situation où les deux verres seront de forme différente. Le même enfant Coc n’hésitera pas une seconde à soutenir qu’il y a plus dans L que dans P (A ayant été transvasé dans L en même temps que B l’était dans P) « parce que c’est tout petit (=plus allongé) et ici (dans P), c’est plus gros ».

A un deuxième stade (= intermédiaire), les réponses des enfants se font hésitantes ou, autre indice, oscillent selon que la centration ou leur attention se portent sur tel ou tel élément de la situation (par exemple sur l’une ou l’autre caractéristique des récipients, ou encore sur un possible retour au point de départ, sur le souvenir de ce point de départ, sur le procédé de correspondance terme à terme, etc.), ces déplacements d’attention entraînant des modifications dans les réponses données à la question de conservation ou non de l’égalité numérique, donc du nombre. Cette évocation changeante de différents aspects de la situation pourra les conduire à ne plus affirmer aussi franchement la non-conservation, troubler qu’ils peuvent être par les possibles qui s’ouvrent à eux, les contradictions qui peuvent en résulter, voire même les conduire à formuler des réponses peu sûres de conservation.

Si, par exemple, après une réponse impliquant la non-conservation, l’expérimentateur (E) demande ce qui se passera si les perles de chacun des deux récipients différents étaient utilisées pour faire des colliers, les enfants pourront admettre qu’il y aura la même chose de perles dans chaque collier, tout en continuant d’admettre qu’il y a plus de perles dans le verre L (pour un exemple, voir Marg 5 ½ ans, Genèse du nombre, pp. 48-49) ! La question sur le collier peut ainsi conduire le sujet du stade II à se décentrer de l’aspect le plus prégnant perceptivement, à savoir le niveau des perles dans chacun des deux verres, pour juger au moins momentanément que « les deux colliers seront la même chose longs » (Ari, 5 ½ ans, id., p. 49). De même dans le cas où le procédé de correspondance terme à terme est utilisé pour remplir deux verres différents, Tis (5 ans et 1 mois) soutiendra d’abord que le verre L contient plus de perles ; mais il suffira que (E) lui demande comment ils ont mis les perles dans les verres pour qu’il juge que (E) et lui ont mis la même chose « parce qu’on a mis un chaque fois les deux [= (E) et l’enfant] » ; mais cette dernière affirmation ne se sera pas maintenue, car une simple centration sur les niveaux différents des deux verres le ramènera à sa première affirmation selon laquelle il y a plus de perles là où le niveau est plus haut (id., p. 50). [3]

Enfin, au troisième stade, l’enfant est convaincu que le versement des perles dans un verre différent ne modifie en rien le nombre de perles, et donc qu’il y en a toujours la même chose, puisqu’avant c’était la même chose, que l’on a rien ajouté et rien enlevé, que l’on a mis en même temps, ou encore que le niveau des perles peut certes être moins élevé dans le verre de départ, mais comme celui-ci est plus large, ce que l’eau perd en hauteur elle le gagne en largeur.

Ces arguments sont recueillis lorsque l’expérimentateur demande à l’enfant de justifier son affirmation selon laquelle la quantité d’eau ne change pas quand on verse le liquide dans un récipient de forme différente (moins large et plus haut, par exemple) : l’enfant qui a atteint le niveau opératoire démontre par ses réponses qu’il a en vue non seulement l’argument d’identité préalable (garanti à la fois par l’action de correspondance terme à terme et par l’identité de forme des verres et de niveau de l’eau), ou l’argument de réversibilité (on peut remettre l’eau dans le récipient de départ), mais également l’argument de compensation (ce que l’eau perd en hauteur, elle le gagne en hauteur). Les enfants des stades I et II savent bien qu’au départ il y a égalité des quantités et que l’on peut revenir au point de départ. De même, comme le montrent leurs réponses de non-conservation, ces enfants ne manquent pas de prendre en considération les changements de forme et de niveau. Mais c’est seulement lorsqu’ils mettent en rapport l’ensemble des variations de niveau et de formes, ainsi que les trois arguments 1° d’identité initiale, 2° de non modification de la quantité d’eau par ajout ou soustraction d’eau dans l’un des deux verres et 3° de compensation des variations de hauteur et de largeur, que les enfants parviennent à affirmer sans aucune hésitation la conservation de la quantité de perles transférées d’un verre de forme A à un verre de forme différente, ceci alors même qu’il peut sembler qu’il y en a plus dans l’un ou l’autre de ces verres.

En conclusion, en plus de montrer que la progression des réponses des enfants d’un stade à l’autre dans ce problème de conservation d’une quantité de perles est la même que celle des réponses à un problème de conservation de quantités physiques (des liquides en l’occurrence), cette expérience est intéressante en ce qu’elle illustre le fait que, comme l’ont révélé les réponses du 2^ème stade, l’action de correspondance terme à terme (ou biunivoque), qui joue un rôle crucial dans les réponses que les mathématiciens ont apporté au problème de l’origine, de la constitution ou encore de la définition du nombre, ne suffit pas à elle seule à expliquer la genèse du nombre chez l’enfant, quand bien même elle peut ponctuellement aider l’enfant à se décentrer des aspects les plus prégnants et trompeurs livrés par la perception. Comme on le verra dans la suite, seuls le regroupement et la synthèse d’un ensemble d’actions ou de préopérations au départ non ou insuffisamment reliées les unes aux autres permettront à l’enfant d’acquérir la notion mathématique de nombre naturel dont héritera la science arithmétique.

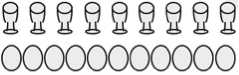
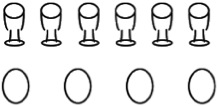
L’épreuve des œufs et des coquetiers

Contrairement à la précédente, cette deuxième épreuve cible d’emblée non seulement le problème de la conservation du nombre, mais celui de la correspondance terme à terme dont il s’agit de connaître le rôle exact qu’elle joue dans la genèse du nombre chez l’enfant.

Dans cette épreuve, la situation standard à laquelle les enfants sont confrontés est la suivante. De faux coquetiers et de faux œufs sont placés en vrac sur une table face à laquelle se trouvent l’expérimentateur E et l’enfant interrogé (les œufs se trouvent dans un panier). E prend alors un à un entre 6 et 10 coquetiers qu’il aligne soigneusement sur la table, à un cm environ les uns des autres, tout en disant à l’enfant de bien regarder ce qu’il fait. Une fois achevée cette action, il demande à l’enfant de faire comme lui, et de placer son tour des œufs pour qu’il y ait la même chose d’œufs (sous entendu : que de coquetiers alignés sur la table) [4]. La suite de chaque entretien dépend, comme on va le voir, de la conduite adoptée par les enfants et qui varie d’un stade à l’autre.

Résultats

Stade I. — Les résultats sont très spectaculaires et significatifs. Lors du premier stade, aucun usage n’est fait de la correspondance terme à terme. Suite à la demande de mettre la même chose d’œufs qu’il y a de coquetiers, les enfants les plus jeunes (4 ans environ) placent certes un à un les œufs devant les coquetiers en faisant en sorte que la ligne des œufs soit égale à celle des coquetiers, mais en les serrant les uns contre les autres de telle sorte que leur nombre est plus grand que celui des coquetiers :

Après avoir demandé à l’enfant s’il est sûr de sa réponse et que celui-ci a répondu affirmativement, l’E lui demande alors de mettre les œufs dans les coquetiers. Les enfants reconnaissent alors qu’ils se sont trompés et qu’il y a plus d’œufs. Une fois les œufs en surplus remis dans le panier, et que cela fait, les enfants reconnaissent qu’il y a la même chose d’œufs que de coquetiers (puisque chaque coquetier contient un œuf et que chaque œuf se trouve dans un coquetier, donc qu’il y a correspondance biunivoque au moins perceptive entre les deux collections), vient la question décisive concernant la maîtrise ou non de la conservation du nombre.

L’E sort un à un les œufs des coquetiers (ou les fleurs des vases) pour les placer un à un sur une ligne devant ces derniers, mais soit en les serrant les uns contre les autres, soit en laissant entre eux un écart plus grand que celui existant entre les coquetiers. La réponse des enfants de ce stade est claire : pour eux, il y a plus d’éléments là où la série est la plus allongée. C’est donc sur une propriété spatiale particulièrement prégnante que les enfants font reposer leur jugement, et il suffit d’alors de modifier la disposition des éléments de manière à rendre prégnante cette propriété pour qu’ils formulent un jugement impliquant la non-conservation du nombre. Cette prégnance de la perception spatiale est même si forte que si E demande aux enfants s’il y a assez d’œufs pour remplir les coquetiers (ou inversement, selon la réponse préalable des enfants, s’il y a assez de coquetiers pour pouvoir y mettre tous les œufs), ils répondent par la négative ou en affirmant qu’ils ne savent pas, ce qui confirme que pour eux la quantité d’œufs a changé ou est susceptible de changer lorsqu’on les éloigne ou les rapproche les uns des autres.

Une épreuve complémentaire permet également de corroborer ce primat de la perception spatiale dans une épreuve portant sur la quantité numérique. Dans cette épreuve, E aligne (par exemple) 7 coquetiers les uns à côté des autres, puis 4 œufs devant les coquetiers, mais de manière à ce que le premier et le dernier de chaque collection soient alignés sur le premier et le dernier des éléments de l’autre collection.

En réponse à cette nouvelle question portant sur l’égalité ou non des deux collections ainsi disposées, les enfants de ce premier stade répondront, comme Zu (4 ans et 9 mois) [5], qu’il y a la même chose d’œufs que de coquetiers et seront tout étonnés de constater ensuite que les 4 œufs ne suffisent pas à remplir chacun des coquetiers.

Ce que montrent ces quelques exemples, c’est que, quand bien même elle n’est pas spontanément utilisée au départ pour établir l’égalité demandée, il y a bien chez ces enfants un début d’utilisation de la correspondance terme à terme pour juger de l’égalité ou de la non égalité numérique de deux collections d’objets, mais que cette correspondance n’est pas strictement numérique, puisqu’elle n’est plus reconnue dès qu’il y a suppression de la correspondance perceptive. En d’autres termes, s’il y a bien une certaine notion de quantité numérique chez ces enfants, cette notion n’est pas suffisamment détachée de la perception de l’espace occupé par chacune des collections comparées pour leur permettre de résister à ce que suggère la centration sur les caractéristiques spatiales, et en particulier sur la seule correspondance ou absence de correspondance optique entre les frontières des deux alignements.

Stade II. — A la différence des enfants du 1^er stade, les enfants du 2^e stade prennent davantage en considération l’action de correspondance terme à terme, et non pas seulement la correspondance perceptive, dans leur jugement sur la conservation ou non conservation de la quantité d’éléments composant une collection soumise à des transformations spatiales. Invités à mettre la même chose d’œufs qu’il y a de coquetiers, ils placent en effet spontanément un œuf devant chaque coquetier. Mais à nouveau, et comme au premier stade, il suffira que l’E écarte ou resserre l’une des deux rangées pour que l’enfant du 2^e stade juge que la plus longue des deux contient plus d’éléments.[6] Cependant, si l’on demande ensuite à cet enfant ce qui se passerait si l’on remettait les œufs (ou les coquetiers) comme il les avait placés au départ, il répondra sans hésiter qu’il y aura à nouveau la même chose d’éléments dans les deux collections, puisqu’avant il en avait mis la même chose (par correspondance terme à terme) et que depuis, on n’en a ni ajouter ni enlever. Par contre, si le même enfant est invité à compter le nombre d’élément de chacun des deux collections, il pourra faire en sorte que le nombre auquel il arrive pour l’une des deux collections s’ajuste à sa réponse de non-conservation (donc sauter un élément dans l’une des deux collections, ou au contraire compter deux fois un élément, et ainsi arriver par exemple à 7 en pointant du doigt le dernier élément d’une des deux collections, et à 8 pour le dernier élément de la deuxième collection) ! [7] Ce qui implique que, là encore, il y a indifférenciation relative de la quantité arithmétique par rapport à une quantité spatiale, en l’occurrence la longueur des rangées.

Toujours chez l’enfant du 2^e stade, il peut arriver qu’en cours d’entretien il juge momentanément que les quantités restent égales après modification spatiale de la longueur de l’une des rangées. C’est le cas dans les situations qui, comme celle des œufs et des coquetiers, tendent à faciliter la représentation de la correspondance terme à terme, et donc la centration sur celle-ci, ou lorsque l’enfant utilise le procédé de comptage appris en famille ou à l’école (pour les jeunes enfants scolarisés), un procédé dont on remarquera d’ailleurs qu’il repose lui aussi sur une correspondance terme à terme entre un élément perçu et un élément énoncé. C’est le cas par exemple de Os (5 ans 10 mois) qui compte 10 vases alignés par l’expérimentateur E, puis qui compte 10 fleurs en même temps qu’il les met une à une dans les vases (voir Genèse du nombre, p. 74). Lorsque E, après avoir sorti et entassé toutes les fleurs que Os vient de mettre dans chaque vase (une par vase), demande à l’enfant s’il y a la même chose ou plus ou moins, celui-ci commence par répondre la même chose « parce qu’il y a 10 fleurs et 10 vases ». Le comptage prime la mesure basée sur les propriétés spatiales. Mais il suffit cependant que E resserre un peu les vases les uns contre les autres et écarte les fleurs pour que Os modifie sa réponse et affirme qu’il y a moins de vases. Les caractéristiques spatiales redeviennent le critère sur lequel l’enfant base sa réponse. Une telle oscillation du jugement est tout à fait typique des réponses des enfants du 2^e stade. La suite de l’entretien avec Os confirme cette insuffisante différenciation entre quantité numérique et quantité spatiale.

En effet, E donne une deuxième collection de fleurs à l’enfant, cette fois des fleurs non plus bleues mais roses (les fleurs bleues précédemment comptées restant alignées et écartées les unes des autres sur la table). Comme précédemment, il demande à l’enfant de mettre la même chose de ces fleurs roses qu’il y a de vases, et Os procède comme il l’a fait auparavant, c’est-à-dire en comptant de 1 à 10 en même temps qu’il met une fleur rose après l’autre dans chaque vase. E sort alors ces fleurs roses et les étale devant les vases toujours resserrés les uns contre les autres, puis il demande à l’enfant s’il y a la même chose ou non de fleurs roses et de fleurs bleues. Os répond affirmativement en justifiant l’égalité par le fait qu’il y en a « 10 ici et 10 là ». Mais interrogés sur le fait de savoir s’il y a la même chose de fleurs roses ou de vases, il répond à nouveau par la négative, alors même qu’il vient de formuler les chiffres de 1 à 10 en mettant les fleurs roses une à une dans chaque vase. On voit ici très clairement que le fait de savoir compter ne suffit pas à formuler un jugement numérique exact quant à la quantité de vases dans l’ensemble que ceux-ci composent. On reviendra sur cette question dans la suite.

Stade 3. — Ce stade se caractérise par la maîtrise incontestable de la conservation des quantités numériques, en même temps que la correspondance terme à terme acquière une nouvelle signification : non seulement elle est d’emblée utilisée par les enfants de ce stade (que ce soit directement ou par comptage) pour construire une collection d’éléments ayant la même chose d’éléments qu’une collection déjà constituée, mais en plus elle devient pleinement logique et non plus empirique en ce sens que, une fois constatée, ses conséquences logiques quant à la quantité d’éléments que contient une collection ne peuvent être annulées par la suppression de la correspondance terme à terme perceptive ou figurale. En raison du sens définitivement purement arithmétique qu’il donne à leur usage de la correspondance terme à terme, ces enfants résistent sans problème à toute suggestion perturbante de l’expérimentateur cherchant à valoriser les modifications d’une quantité spatiale systématiquement utilisée par les enfants plus jeunes pour affirmer la non-conservation d’une quantité d’éléments d’une collection lorsque cette collection n’apparaît plus correspondre terme à terme au modèle de départ.

Ainsi, lorsque l’expérimentateur E, reprenant les arguments par lesquels un enfant du 1^er ou du 2 stade peut justifier son jugement d’inégalité des quantités numériques de deux collections dont ils viennent d’affirmer l’égalité, suggère qu’il pourrait y avoir « plus de coquetiers parce que la rangée qu’ils forment est plus longue que celle des œufs » (ou l’inverse), les enfants du 3^e stade rejettent aussitôt un tel argument en notant que si, en effet, telle collection est plus longue que l’autre, ce fait est compensé par cet autre fait que la seconde collection a des éléments plus resserrés les uns contre les autres. Et ils savent que la seule façon de modifier quantitativement une collection d’éléments est de lui ajouter ou de lui enlever un ou plusieurs éléments.

Jusqu’à maintenant, les expériences concernaient la quantité numérique, c’est-à-dire le nombre cardinal de collections et du rôle joué par la correspondance terme à terme dans la comparaison entre les quantités d’éléments de deux collections ou plus. Voyons maintenant ce qu’il en est du nombre ordinal qui, pour certains mathématiciens, constitue la base du nombre naturel.

II. Le nombre ordinal et son lien avec le nombre cardinal

Commençons par rappeler le lien étroit qui existe entre la notion de nombre cardinal et la notion de classe logique, lien qui conduit assez directement à la définition par Russell de chacun des nombres cardinaux comme étant la classe des classes entre lesquelles une correspondance un à un peut être établie. Au contraire, et comme son nom le suggère, la notion de nombre ordinal a des liens avec la notion logique de relation asymétrique, et donc de l’opération logique qui a été présentée dans l’avant-dernier cours. Dans ce cours sur la sériation logique, nous avions pu découvrir les étapes franchies par le sujet pour acquérir la notion de relation asymétrique, ainsi que l’utilisation de la méthode opératoire qui atteste la pleine compréhension de cette notion chez le sujet (à savoir, prendre récursivement la plus petite —ou la plus grande— de toutes les baguettes restantes pour la placer à la suite de celles déjà posées).

Pour étudier la genèse de la notion de nombre ordinal (ou les notions de 1^er, de 2^e, etc.), plusieurs épreuves sont utilisées qui toutes reposent sur la notion de correspondance ordinale entre deux séries de relations asymétriques. Déjà dans leur recherche sur le développement de la sériation logique, Piaget et Szeminska avaient pu mettre en évidence le fait suivant : les enfants qui savent résoudre opératoirement le problème de la sériation des baguettes peuvent simultanément résoudre les tâches de correspondances ordinales. En effet, si juste après qu’un enfant vient de sérier, en utilisant le procédé opératoire décrit ci-dessus, une dizaine de poupées (P) en bois de hauteur différente, on lui redonne les mêmes poupées mais aussi 10 balles B (ou 10 cannes) toutes de grosseur ou hauteur différente, en lui demandant de faire en sorte que chacune des poupées P ait une canne ou un balle B qui corresponde à sa hauteur, cet enfant, qui est donc au niveau opératoire, n’aura aucune peine de le faire en utilisant à nouveau le procédé opératoire qu’il a spontanément utilisé pour réaliser sa première sériation. Sa démarche démontre qu’il sait d’emblée pouvoir mettre en correspondance sériale, par ordre de grandeur, chacun des couples de termes des deux collections (et éventuellement d’ailleurs d’écarter un ou plusieurs termes de la seconde série, s’il s’avère qu’il y a plus de B que de P, ou inversement). — Quant aux enfants du deuxième stade qui parviennent à construire empiriquement, c’est-à-dire par tâtonnement, une sériation simple, ils pourront de la même manière trouver les éléments de la 2^e série d’objets correspondant aux éléments de la 1^ère, progressivement guidés qu’ils sont par la correspondance visuelle entre les éléments des deux séries.

Si avec la tâche précédente, on reste donc dans le contexte de la seule sériation asymétrique logique (ou prélogique), qu’elle soit simple ou qu’elle fasse intervenir une correspondance visuelle entre les éléments de deux séries ou plus, une simple complication du problème va permettre de révéler le parallélisme entre le développement de la sériation logique et l’acquisition de la notion de nombre ordinal. Voilà cette complication :

Après qu’un enfant a réussit à construire par un procédé empirique ou au contraire opératoire une double sériation du genre de celle dont nous venons de prendre connaissance, l’(E) peut écarter l’une des deux séries de P et resserrer l’autre (= B) puis ceci fait demander à cet enfant à quel poupée P correspond alors telle ou telle balle B.

Or les résultats sont nets : les enfants qui n’ont d’autres moyens que le tâtonnement empirique pour résoudre le problème de correspondance sériale ne parviennent pas à retrouver dans la série B le correspondant d’un élément quelconque de la série P. Voilà un exemple du type de comportement que peut manifester un enfant parvenu au 2^e stade de la sériation.

Le stade II. Un exemple. — Après que Lie (5 ½ ans) a sérié par tâtonnement les poupées P et établi par le même procédé empirique la correspondance avec les balles (le résultat n’est pas complètement exact : il y a par exemple interversion des poupées P6 et P7), l’expérimentateur (E), après avoir écarté les balles, demande à l’enfant s’il y a « encore la même chose de balles que de poupées ». Conformément aux réponses du 2^e stade, Lie répond : « il y a plus de balles ». « Il y a combien de balles », lui demande alors E. « Dix », répond l’enfant après les avoir comptées ; quant aux poupées, elles seraient moins que 10, mais Lie reconnaît, après les avoir également comptées, qu’il y en a aussi 10. Vient alors la suite de l’échange (je cite un extrait) qui se rattache cette fois au problème de la notion de nombre ordinal. E demande à Lie :

« Alors, pour cette poupée (P5) quelle est la balle qui va ? — (Lie montre B7.) — Et pour celle-là (P1)? (Il montre B1.) » Il montre de même B10 pour P10, B9 pour P9 ; B8 pour P8, B7 pour P7, mais lorsque l’on saute d’une poupée à l’autre, il montre systématiquement B8 pour P7, B2 pour P3 (parce qu’il a pointé du doigt les 2 éléments antérieurs à P3, soit P1 et P2), B4 pour P3 (il pointe cette fois les 3 éléments antérieurs à B4 pour trouver la correspondance avec P3), etc.

Lorsque l’on reprend la correspondance graduelle de P10 à P1, il répond juste (en pointant toujours du doigt), puis lorsque l’on saute à nouveau, il retombe dans la même erreur systématique. (Voir La genèse du nombre, p. 147).

Dans cet exemple, Lie parvient certes à désigner correctement chaque B correspondant à chaque poupée de rang P1, P2, etc., mais ceci seulement si l’expérimentateur l’interroge en procédant dans l’ordre P1, P2, etc., alors que si E désigne une poupée quelconque à l’intérieur de la série des P, l’enfant procède en se fiant à des approximations (par exemple désigner B7 pour P5), ou encore à des report de comptage erronés.

Pour trouver sans se tromper l’élément correspondant dans la collection des B, la solution la plus simple et qui semble la plus évidente serait bien sûr d’utiliser le nombre cardinal de la série partielle d’éléments qui contient la P de tel rang, c’est-à-dire de tel nombre ordinal. C’est là un procédé qui découle immédiatement du savoir spontané que nous avons de l’existence d’une correspondance entre nombre cardinal et nombre ordinal. Or Lie, qui a spontanément compté les poupées, a certes l’intuition d’un tel procédé, mais sans véritable maîtrise opératoire qui seule l’empêcherait d’identifier le 2 cardinal avec le 3 ordinal).

D’autres enfants de ce même 2^e niveau, ne se contentent pas de pointer du doigt les éléments en jeu, mais les comptent effectivement lorsqu’il s’agit de trouver tel élément de l’une des deux séries correspondant à tel élément de l’autre série. Ce qui ne les empêchent pas d’aboutir à des solutions incorrectes. C’est le cas par exemple de Chou (7 ans ; voir Genèse du nombre, p 148) à qui l’on demande de trouver l’élément correspondant à P6 : il compte le nombre cardinal encore tout empirique[8] (=5) de P qui le précède, mais ensuite compte les 5 premières balles en désignant le dernier élément de ce décompte (soit B5) comme le correspondant de P6.

En bref, chez l’enfant du deuxième stade, on constate que, faute de coordination opératoire avec ce qui n’est encore qu’un prénombre cardinal, le (pré)nombre ordinal d’un élément quelconque se perd ou varie dès qu’il n’y a plus le support de la perception (le 5^e d’une collection non écartée peut devenir le 7^e de la même collection dont les éléments sont simplement un peu plus éloignés les uns des autres etc.). Or un nombre (qu’il soit cardinal ou ordinal) qui varie selon la configuration perceptive, et cela alors même que l’enfant sait qu’aucun élément n’a été ajouté à l’ensemble ou à la série en question ne peut être considéré comme un nombre au sens plein du terme ! C’est la raison pour laquelle Piaget adoptera la solution de qualifier ce nombre d’intuitif, de figural ou d’empirique, par opposition au nombre opératoire qui n’apparaît qu’au 3^e stade, avec la maîtrise des opérations les plus simples qui le concernent et qui forment groupe, comme nous allons le voir.

En bref, toujours, ce 2^e stade se caractérise également par une absence de lien stable entre les notions de rang et de quantité chez les enfants qui n’ont intériorisé qu’une forme toute scolaire de dénombrement, ou dont le seul procédé de résolution reste la mise en correspondance perceptive des quantités et des rangs.

Examinons maintenant les comportements des enfants du 3^e stade, en ce qui concerne l’acquisition du nombre ordinal en liaison avec l’acquisition du nombre cardinal.

Stade III. — Dès que les enfants parviennent au 3^e stade de construction des opérations propre à la logique des relations asymétriques et donc à résoudre sans difficulté des problèmes de sériation, ils parviennent également à trouver la juste correspondance ordinale entre une poupée quelconque du problème précédemment décrit et la balle qui lui convient, et ceci en recourant au nombre cardinal de la série partielle dont cette poupée est le dernier élément (et donc en comptant le nombre cardinal de la série des nombres ordinaux qui aboutit au n^ième rang occupé par la poupée dont il s’agit de trouver la balle qui lui correspond). Ils sont alors guidés par leur notion opératoire (et non plus empirique ou intuitive) de nombre, dont on verra un peu plus loin qu’elle est toujours double, car combinant les opérations de classification et de sériation. Examinons donc quelques exemples de comportement de 3^e stade, en commençant par le cas de Bos, un enfant de 6 ans et demi qui est confronté à un problème de correspondance ordinale après avoir mis en correspondance la série croissante des poupées P et des balles B et après que l’expérimentateur E a écarté les balles et ainsi brisé la correspondance visuelle entre chaque pair d’éléments successifs des deux séries. Voilà un extrait du protocole tel qu’on peut le lire à la p. 153 de La genèse du nombre :

« Cette balle (B8) est à qui ? (Bos montre P8.) — Comment tu sais ? — Je vois les 3 (B10, 9 et 8), et là aussi (P10, 9 et 8). — Et celle-ci (B6) ? — A celle-là (P6), parce qu’avant il y avait 8 et c’est sauté à 6 (il a donc compté les balles 1-6). — Qu’est-ce qu’on a fait ? — Avant il y avait 3 (10, 9 et 8), et maintenant on a sauté à 5 (il compte cette fois les balles 10, 9, 8, 7, 6 et les poupées 10-6 et montre à nouveau P6 et B6). »

On voit bien avec cet exemple comment l’enfant de niveau opératoire recourt immédiatement au nombre cardinal pour trouver le n^ième élément demandé (et donc pour résoudre une problème ordinal).

Il en va de même dans une deuxième épreuve lors de laquelle les séries ne sont pas disjointes, mais simplement présentées en ordre inverse l’une par rapport à l’autre. Le même sujet n’a aucune peine à retrouver, par comptage, le n^ième élément depuis la droite de la série inversée lorsqu’on lui désigne le n^ième élément depuis la gauche de la série non-inversée.[9]

Dans les faits donc, même si, considéré sous l’angle purement logique, il est possible (voir B. Russell par ex.) de livrer deux définitions indépendantes du nombre cardinal et du nombre ordinal, de fait, pour résoudre n’importe que problème dans lequel il s’agit soit de trouver le nombre ordinal de l’un des éléments d’une série, soit de trouver le nombre cardinal d’une collection, le sujet ne peut pas, en général, ne pas tenir compte du caractère à la fois ordinal et cardinal de la série des nombres naturels lorsqu’il s’agit de trouver le nombre cardinal d’une collection d’éléments ou le nombre ordinal d’un élément d’une série ! Seules exceptions que nous avons rencontrées dans le contexte des anciens travaux sur la psychologie du nombre chez l’animal : les cas où il y a une correspondance figurative aisément reconnaissable entre de petites collections (4 objets d’une première collection et 4 autres objets d’une autre collection par exemple), ou une correspondance de rang entre les éléments de petites séries entre lesquelles une telle correspondance peut aisément être établie (par exemple entre une première série de 4 sons qui se succèdent et une autre série de 4 sons), exceptions que l’on retrouve dans de récentes expériences au cours desquelles des chercheurs ont cru pouvoir contredire Piaget en montrant que de jeunes enfants et même des bébés se montrent surpris lorsque, après avoir vu 3 poupées venir se cacher derrière un écran, ils n’en voient plus que deux lorsque l’écran est levé. [10]

Ce que semblent démontrer ces dernières expériences, c’est l’existence d’une connaissance innée élémentaire de la numérosité. Une telle existence s’explique d’ailleurs aisément : il est utile à la survie animale de percevoir le nombre d’éléments d’une collection d’objets perçus. Mais, à moins que l’hérédité ait pourvu telle ou telle espèce d’un compteur inné d’éléments, l’arithmétique disons animale se limite à 1, 2, 3, 4, et ceci sans conservation opératoire, puisque chacune de ces numérosités se diluent dans le beaucoup lorsque les collections présentées ne se limitent pas à 1 ou 2, ou 3, ou 4 ou peut-être 5 éléments.

Cette connaissance prénumérique fournit certainement un point de départ au construction du jeune enfant, mais celui-ci aura bien du chemin à faire pour parvenir à cette notion de nombre entier sous son double aspect de cardinal et d’ordinal, dont les expériences classiques de Piaget et de Szeminska exposées dès 1941 dans La genèse du nombre chez l’enfant ont permis de retracer les principales étapes. Ces expériences ont ultérieurement été complétées par de nouvelles recherches réalisées cette fois au Centre international d’épistémologie génétique (créé, comme on l’a vu, au milieu des années 1950). Une première série de ces recherches complémentaires s’est déroulées dans les années 1950 et au début des années 1960. Cette première série à permis de réviser, d’affiner et de compléter les recherches des années 1930. Une nouvelle série a été réalisée dans les années 1970, ceci dans le contexte des études non plus sur la genèse des catégories de base de la connaissance (dont le nombre), mais sur les mécanismes de construction des structures opératoires sous-tendant le fonctionnement de ces catégories (par exemple, l’étude du mécanisme d’abstraction réfléchissante [11] permettant de passer d’une étape à une autre, mécanisme qui lui-même passe par différentes étapes).

Avant de conclure ce cours sur la construction du nombre, il vaut la peine de s’arrêter sur deux recherches des années 1950 réalisées par Pierre Gréco, l’un des plus proches collaborateurs de Piaget, dans la mesure où elles mettent en évidence des aspects de cette construction jusque-là restés dans l’ombre.

B. Recherches complémentaires

1. L’arithmétisation progressive de la série des nombres naturels

Plusieurs expériences conduites au CIEG dans les années 1950 montrent comment l’enfant de 6-7 ans environ, qui maîtrise opératoirement le nombre jusqu’à 8 ou 9 environ, ne parvient pas immédiatement à généraliser ses jugements sur les propriétés des nombres (dont la conservation) au-delà de ce nombre. Ceci prolonge dans une certaine mesure les oscillations de jugement que l’on peut constater au deuxième stade de la genèse du nombre décrit précédemment. En d’autres termes, la notion de nombre opératoire fraichement acquise par l’enfant de 6-7 ans est refoulée dès que les propriétés spatiales deviennent à nouveau prégnante en raison du nombre plus élevé d’éléments d’une collection. Ce sont les résultats de telles expériences, dont celle mise en œuvre par Pierre Gréco sur « Les différences de deux »[12] qui ont conduit Piaget à parler d’arithmétisation progressive de la suite des nombres naturels.

Le problème posé aux enfants dans cette expérience est le suivant (ce problème a été suggéré par Piaget). La première partie d’une série A, B, C, D, etc. de collections de jetons est construite par l’enfant avec l’aide de l’expérimentateur. Par exemple, un enfant peut construire la suite de collections : A = 4 jetons, puis B = 5 jetons, puis C = 6, etc., jusqu’à une collection E de 8 jetons, ou H de 11 jetons. L’expérimentateur construit la fin de la série sur le même principe, ceci à partir de la collection L (= 15 jetons dans cet exemple). Un vide est laissé entre la partie construite par l’enfant et celle réalisée par l’adulte.

Après que l’expérimentateur se soit assuré que l’enfant a bien compris le principe de construction des deux parties de la série, il le confronte au problème suivant : trouver combien de jetons il faut ajouter à telle ou telle collection (par exemple A) de la série pour que cette collection ait le même nombre d’éléments que la collection qui se trouve deux rangs plus loin dans la série (dans cet exemple : C).

Voilà l’extrait d’un entretien au cours un enfant, Mick (5 ans et 7 mois), est confronté à ce problème :

[L’expérimentateur désigne A à Mick, et lui demande combien il faut ajouter de jetons à A pour avoir la même chose dans les collection A et C. L’enfant répond tout à fait correctement : « ben, deux de plus » … Et voilà la suite du protocole telle qu’on la trouve à la page 176 de Problèmes de construction du nombre :]

« Et pourquoi? — Parce que là c’est 4, et là 6. — Et comment tu sais que c’est 4, ici [A] ? — Je le vois. — Et ici [C] ? — 6 — Comment tu sais? — Je compte: 4, 5, 6 (il montre successivement A, B, C). — Bien, et si on prend celui-ci [B] et puis, pas celui d’après, mais celui qui vient encore après [D]? — 2 aussi. — Pourquoi? — Parce que c’est 5, et là [D] 7 (exact). — Et avec [C] et [E] ? Encore 2, parce qu’on saute toujours un paquet (on ne peut obtenir d’explication plus précise).

— Bon, on va en prendre par là (gde série) : maintenant je prends [L], et puis on saute [M] et on prend [N] (…[combien faut-il ajouter de jetons ?]…). — 3. — Pourquoi 3 ? — (geste d’ignorance). — (On vérifie et il reconnaît avec quelque désappointement:) Ah! non, ça fait encore 2 !
— Ça t’étonne? — (Silence, puis:) On avait sauté des paquets (se rapporte sans doute à l’interruption entre E et L, et non au paquet M « sauté »). — Et maintenant [M] et [O] ? — 3 ! — Pourquoi? — Parce qu’il y a beaucoup. — Où? — Là [M] et là [O]. — (Après vérification, déception, puis enthousiasme de découverte.) Et pour [N] et [P] ? – 4 ! — Comment tu sais ? — Parce qu’on a sauté un paquet [0] — Mais avant, on sautait aussi un paquet et ça faisait 2. — Oui, mais là, c’est des gros. …

On constate ici que, selon le nombre d’éléments en jeu, un écart numérique entre deux collections n’a pas la même valeur selon que l’on se trouve dans la petite série ou dans la grande. En d’autres termes, ce n’est que dans les petites collections que l’enfant parvient à « cardinaliser » correctement le nombre d’éléments qui séparent deux nombres ordinaux.

Dans son introduction au volume des Etudes d’épistémologie génétique portant sur les Problèmes de construction du nombre, Piaget tire deux conclusion de ce type de résultats (d’autres recherches vont dans le même sens que la précédente) : 1° une valorisation certes indirecte de l’apport de l’entourage, et 2° une extension de la solution antérieure apportée au problème de l’origine du nombre opératoire. Voilà ce qu’il écrit à la page 19 de cette introduction :

[…] la suite apprise des nombres imposée par l’entourage adulte avant la compréhension des structures numériques, semble ne se structurer que par paliers progressifs ou par zones, sans généralisation immédiate aux nombres 7-15 ou 15-30, etc., de ce qui est compris pour le 1^er palier de 1 à 7 ou 8. Nous nous trouvons […] en présence d’un processus beaucoup plus profond et plus général, que l’on pourrait désigner du terme d’arithmétisation progressive (et par paliers) de la série des entiers, connue verbalement avant que d’être comprise. Ce qui reviendrait à dire que, si le nombre résulte, selon notre hypothèse, d’une synthèse des emboîtements de classes et de la sériation, cette synthèse ne s’effectue pas en une fois mais à la manière d’une intégration graduelle (au sens psychologique du terme).

Je reviendrai dans les conclusions de ce cours sur l’hypothèse indiquée ici, voisine de la combinaison des notions de cardinal et d’ordinal dont il a été question précédemment. Notons pour l’instant que cet extrait contient une affirmation quelque peu équivoque : les premiers nombres seraient « imposés par l’entourage » et n’auraient pas de valeur de connaissance autre que « verbale » (répéter ce qui été entendu et appris). Faut-il en déduire que Piaget rejette (pour raison de « verbalisme ») un tel apprentissage imposé de la suite de ce qui ne saurait être déjà des nombres à proprement parler ? Pas forcément… La suite de l’affirmation montre en effet que Piaget ne sous-estime pas cet apport, dans la mesure où en résulterait chez l’enfant un travail intellectuel qui, même de portée très limitée, relève déjà de cette « synthèse entre des emboîtements de classes et de la sériation » que l’extrait suivant précise un peu :

[On peut voir] « dès ce niveau [= avant 6 ans] la spécificité des quasi-structures numériques, qu’on ne saurait réduire ni à des préclasses, ni à des prérelations seulement, mais qui témoignent sans doute d’un début de synthèse, entre elles deux (sans donc atteindre le palier qui sera caractérisé par la synthèse complète entre les groupements eux-mêmes de classes et de relations, engendrant les premières structures proprement numériques) ». (id. p. 23)

En d’autres termes, Piaget ne nie pas l’existence d’un « prénombre », ou mieux d’un « protonombre »[13] avant le nombre opératoire, protonombre que, déjà, on ne peut réduire ni aux « protorelations » ni aux « protoclasses » logiques, mais qui contient des aspects emprunts aux unes et aux autres, au moins chez le jeune enfant à qui l’adulte a « imposé » une première confrontation avec la suite des nombres. Piaget connaissait suffisamment bien l’histoire de la pensée humaine pour savoir que des enfants livrés à eux-mêmes, donc en l’absence de toute transmission sociale des connaissances, n’iraient guère au-delà de la connaissance des compétences numériques (ou protonumériques) observées chez les grands singes, ou encore les corbeaux, etc.

En un mot, s’il convient de se méfier de tout verbalisme dans les apprentissages imposés, cela ne signifie pas que tout apprentissage imposé, même verbal, soit vain.

2. Le nombre comme quotité et le nombre comme quantité

C’est dans la même série de recherches sur la construction du nombre que Gréco a mis en lumière un fait dont on trouve déjà des traces dans les observations présentées dans La genèse du nombre (1941) mais qui n’avait pas retenu l’attention de Piaget. [14] Commençons par rappeler le résultat principal des recherches sur la conservation du nombre. Le jeune enfant n’admet pas que le nombre d’une collection d’éléments se conserve lorsque l’on effectue une simple transformation spatiale de la collection (sans ajout ni suppression d’éléments) : le simple allongement d’une suite de jetons entraînerait un accroissement de leur quantité par rapport à une même série qui ne subit pas de transformation, alors même qu’une correspondance terme à terme a été initialement constatée entre les deux collections conduisait l’enfant à admettre leur égalité quantitative de départ. Mais si on demande à un enfant de 5-6 ans si le nombre lui-même a changé, il peut répondre négativement, comme dans l’exemple suivant (extrait de la recherche de Pierre Gréco sur « Quantité et quotité, nouvelles recherches sur la correspondance terme à terme et la conservation des ensembles » [15]) :

Tib (4 ; 11). [Après qu’il a affirmé que la série allongée a plus de jetons parce que «y en a un qui dépasse», Tib répond de la manière suivante aux questions de l’expérimentateur:]. « Est-ce qu’on peut remettre comme avant ? — Bien sûr, c’est le même nombre de puces. — Et comme c’est là, est-ce que c’est aussi le même nombre [donc avec la série allongée]? — Oui, le même nombre, mais y a plus en bas, parce qu’il y en a un en trop. » (op. cit., p. 5)

Cette réponse est loin d’être isolée ! Lorsque Piaget rencontrait des réponses de même type, il ne s’y arrêtait pas (voir plus haut) ou les assimilait à un simple apprentissage verbal. En examinant finement ce qui intervient dans les réponses d’enfants tels que Tib, Gréco a le mérite de relever que même s’il y a en effet risque de verbalisme lié à un simple apprentissage verbal de la suite des nombres, cela n’est pas forcément le cas. L’apprentissage de la suite des premiers chiffres peut entraîner la construction d’un schème complexe d’action : émettre une suite de son tout en pointant l’un après l’autre les éléments de la série dénombrée ou en ajoutant un nouvel élément après ceux déjà placés. Ceci suffit à amener le sujet à créer une première notion de nombre (qui, tout en s’appuyant sur elle, va au-delà de la perception de la numérosité des petites collections) : le nombre comme quotité, ainsi que la désigne Gréco. Sa présence est attestée par les réponses que donnent ces enfants à la question « combien ? ». Ainsi Tib affirme sans hésiter qu’il y a « le même nombre » dans les deux séries de jetons, tout en soutenant que la quantité de jetons dans la série la plus écartée est plus grande du simple fait qu’il y a (apparence trompeuse) un jeton de trop dans cette série. Le fait que l’enfant qui affirme la conservation de la quotité soutient en même temps la non-conservation de la quantité révèle par la même qu’il n’a pas encore complètement isolé le nombre cardinal des propriétés spatiales de la collection qu’il a sous les yeux.

Conclusion

Les quelques expériences présentées ci-dessus montrent que, bien que le bébé a certainement déjà un certaine capacité de reconnaître la numérosité de petits ensembles ou de petites collections d’éléments, ce n’est pas avant 6-7 ans qu’apparaît la notion de nombre naturel au sens usuel du terme, qui seul peut servir et a certainement servi de base à la construction de la science arithmétique, dans la mesure où cette notion différencie complètement les propriétés cardinales et ordinales des caractéristiques spatiales d’un ensemble d’éléments, et par là permet l’indépendance et le regroupement des opérations numériques (l’addition et la soustraction). On a vu au passage comment cette acquisition, ainsi que la propriété de conservation du nombre qu’elle implique, sont liées à la reconnaissance de trois types de considérations mis en lumière par les arguments que l’on obtient lorsqu’on demande aux enfants de niveau opératoire de justifier leur jugement de conservation, ou lorsque l’on formule des contre-suggestions dans le but de vérifier la solidité de ce jugement : l’identité, la réversibilité et la compensation. L’enfant opératoire reconnaît immédiatement, ou après une courte réflexion, qu’une collection dont on éloigne ou dont on rapproche les éléments les uns des autres conserve le même nombre d’éléments dans la mesure où (1) on ne lui en a pas ajouté de nouveaux, (2) que si l’on en ajoute on peut revenir au même nombre en réalisant une opération inverse annulant complètement la première, et enfin (3) que le fait que des éléments qui paraissent en surplus dans une collection dont on a écarté les termes sont compensés par le plus grand nombre d’éléments présents dans l’espace plus réduit de la collection dont les composants n’ont pas été éloignés les uns des autres.

Enfin, et pour conclure ce chapitre sur la genèse du nombre, revenons sur la thèse centrale développée par Piaget quant à la nature même du nombre, conçu comme le résultat de la synthèse ou de la fusion des opérations d’inclusion de classes et de sériation des relations logiques (ou, pour le nombre préopératoire non encore pleinement différencié de l’espace, de la synthèse des préopérations d’inclusion et de sériation prélogiques).

Pour cerner ce processus de synthèse proposé par Piaget à la suite de ses maîtres Arnold Reymond et Léon Brunschvicg, prenons par exemple une collection de 7 unités (en rappel de l’argument de Kant selon lequel le nombre 7 est issu de l’addition de 1 élément à une série de 6 éléments, elle-même issue de l’addition de 1 à une série de 5 éléments elle-même issue… etc.). Cette collection de 7 contient la collection de 6, qui elle-même contient celle de 5, etc. jusqu’à la collection de 2, contenue dans celle de 3 et contenant celle de 1. Mais, comment distinguer la collection de 7 de celle de 6 alors même que tous les éléments sont pareils (sont des 1) ?

En logique, on peut distinguer les éléments d’une classe A (tous les carrés appartenant à un ensemble de carrés noirs par exemple) d’un autre élément (un autre carré) qui possède une caractéristique que les A ne possèdent pas (dans cet exemple une couleur différente, blanche par exemple), ce qui permet de construire la classe emboîtante A+A’=B (A’ étant composée des éléments de B qui ne partagent pas la caractéristique commune réunissant les A). Par contre, si l’on ajoute un carré noir à la classe A, cette classe n’est en rien logiquement modifiée, contrairement à ce qui se passe pour les nombres (5)+(1)≠(5) : la classe des carrés noirs reste la classe des carrés noirs si on lui ajoute un carré noir, en d’autres termes, A = A.

Mais, s’il n’y a aucune différence entre les unités numériques de la collection 7 et les unités numériques de la collection 6, comment distinguer l’élément nouvellement ajouté aux 6 éléments ? La classe de 7 ne se distingue logiquement pas de la classe de 6. Certes, on peut bien utiliser la correspondance terme à terme ? Mais comment établir une telle correspondance alors que l’espace n’entre pas dans le concept de nombre ?

La thèse de Piaget, que conforte les observations qu’il a pu faire du parallélisme d’acquisition des notions de nombre cardinal et de nombre ordinal est que l’enfant y parvient certes en s’appuyant sur l’espace, mais surtout en considérant que le 1 (nombre cardinal) ajouté à la collection de 6 (nombre cardinal) unités déjà construite devient le 7^ème (nombre ordinal) élément de la nouvelle collection de 7 (nombre cardinal) unités qui inclut la collection de 6 unités qui elle-même se distinguait de la collection de 5 grâce au 6^ème élément ajouté à cette dernière, etc., jusqu’au nombre 2, cardinal de la collection de 2 unités qui se distinguait de celle de 1 grâce à son 2^ème élément venant s’y ajouter.

Plus brièvement dit, les unités de chaque collection numérique sont distinguées les unes des autres grâce à l’ordre ou sériation logique que l’on introduit entre elle dès l’ajout de 1 à {1}, jusqu’à l’ajout de 1 à {1, 1, 1, 1, 1, 1…}.

Inversement, le 5^ème élément d’une série se distingue du 4^ème, parce que la collect. {4} des éléments auquel il s’ajoute contient un élément de plus que la collection {3} auxquels s’ajoutait le 4^ème. Etc.

C’est donc bien la synthèse, la fusion ou la coordination entre les opérations (ou préopérations) d’emboîtement et de sériation qui sous-tend les réponses des enfants aux problèmes ou questions qu’on leur pose par des épreuves telles que celles précédemment exposées.

Une illustrations permet de résumer cette synthèse entre l’emboîtement (décrit par les ovales) et l’ordre, décrit par la position successive des éléments ajoutés :

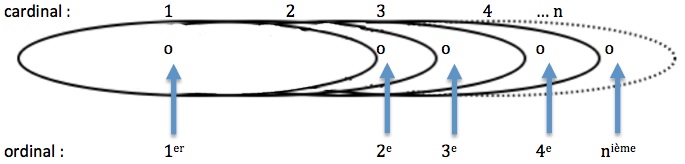
Ce qu’ont montré les expériences résumés ci-dessus, c’est que la correspondance terme à terme des éléments successivement posés ne suffit pas à garantir la conservation du nombre si par ailleurs l’enfant n’a pas à l’esprit l’idée que le tout précédemment construit se conserve (est emboîté) dans le nouveau tout. Et en sens inverse, que l’ajout un nouvel élément ne suffit pas à composer une totalité autre que celle déjà construite, si l’enfant ne retient pas l’idée que ce nouvel élément n’est pas le même que ceux précédemment ajoutés et auxquels il est pourtant identifié (ils sont tous des 1 et ce qui les distingue n’est que le caractère successif de chacun de leur ajout).

En d’autres termes, ce que corroborent les observations psychogénétiques, c’est que, à l’encontre des conceptions des mathématiciens ou des logiciens qui privilégiaient soit le nombre ordinal soit le nombre cardinal dans leur recherche d’un fondement de la science arithmétique, dans l’évolution de la pensée naturelle, la série des entiers se construit dès le départ par synthèse des préopérations puis des opérations de colligation ou réunion d’éléments (dont on fait abstraction de leurs différences individuelles) et de sériation (permettant de distinguer chacun de ces éléments malgré leur identité logique).

D’où la conception épistémologique que propose Piaget quant à l’origine et à la signification du nombre : du point de vue de son origine, la série des nombres entiers est issue de la fusion des (pré)opérations logique de classe et de relation asymétrique ; et du point de vue de sa signification, tout nombre de la série des entiers est simultanément un nombre ordinal et un nombre cardinal. Quant au passage des préopérations et des préconcepts de nombre, aux opérations et concepts de nombre, il est pour l’essentiel issu de la coordination ou de la synthèse des propriétés et actions d’identité, de réversibilité et de compensation, et donc des régulations qui peuvent intervenir chez un enfant confrontés aux transformations de collections d’objet sur lesquelles portent ses jugements et raisonnements numériques. Il reviendra au logicien J.B. Grize (voir le volume 11 des études d’épistémologie génétique pp. 69-96) de démontrer sur le terrain de la logique elle-même 1° comment le fait de réunir formellement les opérations de la logique des classes et de la logique des relations asymétriques fait tomber les restrictions des groupements logiques (loi de tautologie selon laquelle A+A=A, associativité limitée, etc.), et donc 2° comment la disparition de ces limitations ou restrictions permet d’attribuer à la structure opératoire issue de cette synthèse des classes et des relations des lois de groupe mathématique reconnues dès le 19^ème siècle à la structure des nombres entiers.

__________________

[1] Pour saisir toute la valeur de l’apport de ces deux maîtres, on peut lire, du premier : Logique et mathématique, et du second : Etapes de la philosophie mathématique. Ces deux ouvrages contiennent en germes les thèses principales développées par leur élève (cf. à ce sujet ma thèse de 1984 sur la formation de la pensée scientifique et philosophique de Piaget).

[2] En général, par rapport à toute connaissance, on peut faire trois hypothèses quant à sa présence chez un individu : cette connaissance est soit (1) innée (c’est-à-dire héréditairement transmise à cet individu), soit (2) construite par le sujet, soit (3) acquise par apprentissage empirique individuel, ou par apprentissage social (et notamment scolaire).

[3] Avec ces exemples, on n’est pas loin d’une expérience ultérieure de P. Gréco et dont il sera question plus loin, dans laquelle est mise en évidence une conservation du nombre, mais de la quotité [terme emprunté à Cournot et Couturat, cf. EEG, 13, p. 9] alors même qu’il n’y a pas de conservation de l’égalité des deux collection lorsqu’une simple transformation de l’arrangement spatial est introduite sur l’une des deux collections d’éléments, l’autre restant inchangée. J’y reviendrai après la présentation des travaux de Piaget.

[4] La même expérience peut être faite avec des vases et des fleurs, ou deux collections de jetons de couleur différente, ou tout autres objets familiers aux enfants.

[5] Voir La Genèse du nombre, p. 70.

[6] Un extrait de film présenté sur le site de la Fondation Jean Piaget illustre cette succession de réponses. Pour le visionner, consulter la page suivante du site :

http://www.fondationjeanpiaget.ch/fjp/site/ModuleFJP001/index_gen_page.php?IDPAGE=83&IDMODULE=45.

[7] Cette question du dénombrement ou du comptage et de ce qu’il implique pour l’enfant qui n’a pas encore atteint le stade 3 sera reprise plus loin.

[8] La manière dont Chou comme les autres enfants de ce niveau utilisent ce « nombre » démontre que celui-ci n’a pas encore sa pleine signification arithmétique, c’est-à-dire n’est pas encore pleinement dissocié de la numérosité perceptive ou de la grandeur spatial…

[9] Commenté par Piaget, un extrait du film de J.C. Goretta « L’épistémologie génétique de Jean Piaget » illustre le comportement d’une jeune fille de 9 ans interrogée sur le nombre d’éléments qui suivent le premier élément d’une série, et sur le nombre d’éléments (alors cachés) qui précèdent le dernier élément toujours visible de la même série. Cet extrait illustre la façon dont, après qu’on a demandé à cette jeune fille combien d’éléments succèdent au premier élément et qu’elle a, pour répondre à cette question préalable, simplement comptés ces éléments alors tous visibles, elle coordonne ensuite les notions d’ordre (nombre ordinal) et de quantité (nombre cardinal) pour répondre à une question dans laquelle on lui demande combien d’éléments (alors cachés par un carton) précèdent le dernier élément d’une série de baguettes de plus en plus grandes. Cet extrait peut être consulté sur la page suivante du site de la Fondation Jean Piaget :

http://www.fondationjeanpiaget.ch/fjp/site/biographie/index_gen_media.php?MEDIAID=127.

[10] Cette expérience est présentée dans l’ouvrage de Jacques Vauclair dont il a été question dans les cours sur l’intelligence sensori-motrice.

[11] Je reviendrai lors des conclusions du cours sur ce mécanisme.

[12] Cette expérience est rapportée par Pierre Gréco dans son chapitre sur « Recherches sur quelques formes d’inférences arithmétique et sur la compréhension de l’itération numérique chez l’enfant » (in Problèmes de la construction du nombre, EEG, vol. XI, 1969, pp. 149-213).

[13] Dans la suite, nous utiliserons à nouveau les désignations adoptées par Piaget et qui sont basées sur le préfixe « pré ». Mais ce dernier préfixe pouvant suggérer : avant l’existence de tout nombre (ou de toute logique, pour prélogique), nous utilisons momentanément le préfixe « proto » pour désigner des notions encore en germe de nombre arithmétique ainsi que de classe et relation logiques (« proto » signifiant dans le présent contexte non pas « avant », mais « au début », ou encore dans les premières étapes conduisant à une pleine acquisition d’une notion.

[14] On trouve également des traces de cette distinction entre quotité et quantité dans la recherche sur la genèse de la notion d’âge, chapitre 9 de l’ouvrage sur Le développement de la notion de temps chez l’enfant, réponse de Joc (5 ans ½) au problème de comparaison des âges d’un poirier et d’un pommier (cf. 229).

[15] Cette recherche est exposée dans le 13 volume des Etudes d’épistémologie génétique publié en 1962 et ayant pour objet Les structures numériques élémentaires).