La genèse des opérations logiques concrètes
I. Contexte intellectuel et premiers travaux
II. Recherches sur la classification logique
III. Recherches sur la sériation logique
[Vers: Cours n. 12 — Cours n. 11 — Cours n. 10 — Cours n. 9 — Cours n. 8 — Cours n. 6 — Cours n. 5 — Cours n. 4 — Cours n. 3 — Cours n. 2 — Cours n. 1]
Remarques préalables
Aujourd’hui et lors des deux prochains cours, nous allons traiter un chapitre majeur de l’œuvre de Piaget, à savoir ses recherches de psychologie génétique portant sur le développement de la pensée logique et arithmétique chez l’enfant, entre 4 et 9-10 ans. Nous prendrons ainsi une connaissance relativement approfondie de cette période de développement de l’intelligence liée à ce qu’il est convenu d’appeler la pensée ou l’intelligence opératoire concrète, dans la mesure ou dès 6-7 ans et jusqu’à 9-10 l’enfant construit des systèmes d’opérations qui expliquent le type de raisonnement mis en œuvre lorsqu’il est confronté à des problèmes de logique et d’arithmétique (comme nous le verrons aujourd’hui ou dans les prochaines cours), ou encore à des problèmes de coordination de points de vue abordés lors de notre dernier cours et à bien d’autres types de problèmes, tels que ceux de conservation physique (exemple: la transformation d’une boule de plasticine en saucisse ou en plusieurs morceaux modifie-t-elle la quantité de matière, de poids ou de volume ?). Après cet examen des étapes de construction de l’intelligence opératoire concrète, il restera à aborder une ultime étape de développement de l’intelligence, celle qui concerne l’intelligence de l’adolescent, qui prend une nouvelle forme, en raison, entre autres, de la capacité qu’a ce dernier non plus seulement de concevoir et d’organiser l’univers des représentations concrètes (y compris imaginaires) auquel tout un chacun est confronté dans la vie de tous les jours, mais également des univers basés sur de simples hypothèses, ou encore des ensembles de possibles dont il s’agit de tirer les conséquences ou d’éprouver la cohérence logiques. Ainsi nous aurons parcouru les principales étapes du développement cognitif mis en lumière par Piaget dans ses recherches de psychologie génétique sur le développement de la pensée chez l’enfant et l’adolescent. Mais commençons par un rappel.
Lors des précédents cours, nous avons vu comment, lors des 18 mois qui suivent la naissance et à travers des mécanismes tels que ceux de la différenciation ou de la coordination des schèmes sensori-moteurs, est progressivement construit et structuré l’univers des objets proches —et des personnes— sur lesquels le bébé agit ou avec lesquelles il interagit. Les regroupements des schèmes de placement et de déplacement des objets ou du corps propre, et la permanence des objets auquel ces regroupements conduisent est la première très claire manifestation du rôle déterminant que jouent les compositions structurées d’actions dans le fonctionnement et les réussites de l’intelligence sensori-motrice, c’est-à-dire de cette forme d’intelligence qui agit sur les objets ou les personnes proches pour atteindre des buts pratiques non accessibles sans une réelle et intentionnelle activité de coordination des moyens et des fins,[1] et donc une organisation constituante de l’action propre et des objets sur lesquels elle porte.
Lors de notre dernier cours, nous avons vu en outre comment la représentation (grâce à la construction de la fonction symbolique) intervient dans l’étape finale de cette construction de l’intelligence sensori-motrice en permettant au bébé d’évoquer des actions particulières ayant été (et le plus souvent venant d’être) effectivement réalisées par lui ou par autrui, et d’anticiper les actions à effectuer pour atteindre un but souhaité, ces actions évoquées ou anticipées composant, en lien avec l’action en cours dans laquelle elles s’insèrent, des totalités organisées plus ou moins stables et efficaces.
Nous avons enfin vu comment, à travers l’exemple de la coordination des points de vue, la pensée se libère de l’action propre en donnant naissance à un univers de la représentation qui n’est plus le simple prolongement de cette action, et qu’il s’agit d’organiser progressivement de la même manière que, lors des deux premières années de vie, l’univers de la proche perception s’est progressivement structuré en raison d’une coordination toujours plus riche et poussée des schèmes d’actions sensori-motrices. Un bref aperçu sur les travaux beaucoup plus récents ayant pour objet la capacité de se représenter adéquatement ce que pense autrui montre comment les découvertes de Piaget sur le développement de l’intelligence représentative et plus particulièrement sur la coordination des perspectives spatiales éclairent les réponses des enfants rapportées dans ces travaux. Comme nous allons le voir de manière plus complète en examinant les recherches sur la genèse de la pensée logique et de la pensée arithmétique chez l’enfant entre 4 et 8 ans, ce qui explique l’extraordinaire portée des travaux de Piaget sur la pensée de l’enfant est la découverte que, sous les comportements et les réponses des enfants parvenant à résoudre les multiples problèmes cognitifs auxquels ils sont confrontés, se cachent la présence d’ensembles structurés non plus de schèmes d’actions sensori-motrices mais d’opérations logico-mathématiques et de schèmes opératoires, pouvant organiser et transformer les informations véhiculées par ces problèmes pour aboutir à des solutions ou réponses s’imposant avec évidence car fondées en raison.
Avant de découvrir à travers quelques exemples paradigmatiques de la construction de la pensée logique et de la pensée arithmétique de l’enfant, comment se construisent de telles structures opératoires concrètes et comment celles-ci se manifestent à travers les réponses des enfants à des épreuves créées pour étudier la genèse de l’intelligence, rappelons que les travaux de psychologie génétique sur le développement cognitif doivent une grande part de leur originalité et de leur perspicacité au grand projet autour duquel gravite la quasi-totalité de l’œuvre de Piaget: rendre compte des origines de la raison humaine, et plus particulièrement des fondements naturels des sciences ayant atteint un niveau indiscutable d’objectivité et d’universalité (comme le sont la logique, la science des nombres, la géométrie, ou même la mécanique newtonienne, du moins à une certaine échelle d’observation des phénomènes physiques). L’hypothèse qui est à la base des recherches psychologiques de Piaget est, en effet, que ces sciences reposent sur la raison humaine, qui est antérieure à leur naissance, et dont on peut étudier la genèse par le biais de l’étude du développement de la pensée de l’enfant et l’adolescent (à supposer bien sûr, ce que les faits corroboreront, que cette raison ne soit pas un donné préalable que cette pensée ne ferait que refléter). Mais, comme on a pu l’entrevoir dans notre précédent cours avec l’exemple de la coordination des perspectives spatiales prolongeant et élargissant considérablement le travail de décentration observable dans le développement de l’intelligence sensori-motrice, la pensée de l’enfant, repose à son tour sur cette logique de l’action que manifestent des conduites telles que celle de composer, avec l’aide de la représentation naissante, des déplacements judicieusement coordonnés et enchaînés pour atteindre un but en écartant ou en contournant intentionnellement les obstacles qui empêchent son accès le plus direct — conduites observées non seulement vers 18 mois chez le bébé humain, mais aussi dans de nombreuses espèces animales. De même, les opérations de classification et de sériation logiques, ainsi que la notion élémentaire de nombre dont on va examiner aujourd’hui et dans les semaines qui viennent la genèse, ont également des précurseurs dans le fonctionnement des schèmes sensori-moteurs (par exemple, le classement sensori-moteur des objets, en d’autres termes, le lien implicite d’équivalence reconnu entre des objets en tant que ceux-ci sont assimilés à un même schème d’action, l’ordonnancement ou la sériation des actions dans le temps, ou encore la perception de la numérosité des petites collections d’objets, etc.; on retrouvera quelques exemples plus loin de ce possible ancrage initial de la logique de la pensée dans la logique de l’action). Mais là ne s’arrête pas l’hypothèse de Piaget, puisque, selon lui, la logique à l’œuvre dans les coordinations de l’intelligence sensori-motrice est le point d’aboutissement d’une genèse dont le point de départ se trouvent dans des instincts dont l’examen révèle qu’ils sont eux-mêmes composés de coordinations (innées) d’action qui peuvent être très complexes et qui justifient le fait de parler d’une véritable logique de l’instinct. Enfin, dernière étape de cette régression vers les sources ultimes de la raison et donc des sciences, Piaget ne manque pas de souligner comment les coordinations internes propre aux instincts et aux organes qu’ils impliquent ne sont que l’une des nombreuses sortes de coordination vitale (cf. les rythmes ou les cycles biologiques) qui ont conduit les biologistes à accepter l’idée d’une « logique du vivant » selon l’expression adoptée par le biologiste français François Jacob pour intituler l’un de ses ouvrages[2]. En définitive, si les sciences logiques, mathématiques et naturelles peuvent atteindre le niveau d’objectivité et d’universalité qui les caractérise, c’est certes parce qu’elles multiplient les expériences leur permettant de connaître empiriquement la réalité extérieure, mais c’est aussi et surtout parce que, par l’intermédiaire de la raison humaine, de l’intelligence animale et de la logique du vivant, les cadres logico-mathématiques au moyen desquels elles assimilent, organisent et expliquent cette réalité extérieure sont dès leurs plus profondes racines psychologiques et biologiques en phase avec le réel physique dont sont issues et auquel s’adaptent la vie et la pensée, réel dont la pensée scientifique ne peut que progressivement et sans fin espérer se rapprocher, grâce aux efforts coordonnés de la déduction mathématique qui, de l’intérieur du sujet et de l’organisme, le prolonge, et de l’expérience qui, de l’extérieur, s’y confronte.
Cela rappelé, concentrons-nous maintenant sur quelques-unes des recherches consacrées par Piaget à la psychogenèse de la pensée logique de l’enfant, dont on va voir qu’elles sont constamment dépendantes des interrogations et de la formation épistémologiques de leur auteur, d’où leur originalité, leur perspicacité et leur portée tout à la fois psychologiques et épistémologiques. Conformément à la méthode que nous avons adoptée pour ce cours, nous allons commencer par prendre connaissance du contexte préexistant à partir duquel Piaget a édifié ces recherches.
I. Contexte épistémologique initial et premières recherches psychologiques
1. La logique
Lorsqu’on lit les auteurs de la fin du 19e et du début du 20e siècle, on y aperçoit une double conception ou orientation de la science logique, l’une ancienne, héritée de la philosophie grecque et qui a perdu peu à peu le primat voire l’exclusivité qui lui fut accordé jusqu’au 18e siècle inclus, l’autre qui a démarré avec Leibniz, à la fin du 17e siècle, mais qui a pris son véritable envol au 19e siècle. La première orientation, qui restera longtemps sous-jacente à la science logique même après avoir perdu son caractère prioritaire, conçoit cette science avant tout comme l’art d’atteindre le Vrai et de raisonner correctement à son propos, donc l’art du syllogisme, qui a perdu peu à peu son prestige. Cet art tout entier concerné par le Vrai et les énoncés qui l’expriment, Aristote et les logiciens de son époque l’ont dégagé en étudiant comment l’être humain doué de raison s’y prend pour énoncer des affirmations indiscutables (voir à ce sujet le petit livre de Charles Serrus Essai sur la signification de la logique). Aux yeux de ces auteurs et d’Aristote en tout premier lieu, il ne fallait pas aller bien loin pour développer cette science du Vrai. Ils trouvaient dans les formes mêmes du langage courant, et particulièrement dans la forme prédicative d’affirmation dans laquelle quelque chose est dit du sujet de la proposition, le reflet de cette logique par laquelle l’être humain formule des vérités jugées indubitables. De ce que je sais avec certitude que Socrate est un homme, et de ce je sais que les hommes ont pour essence d’être mortel, je peux en déduire sans l’ombre d’un doute que Socrate est mortel (c’est là une forme bien connue de syllogisme, le syllogisme en bArbArA qui lie déductivement les unes aux autres trois affirmations, dont les deux premières sont les prémisses et la troisième la conclusion). Plus tard, les logiciens ne retiendront de l’analyse de ce genre de raisonnement commun que la technique elle-même qui ne sera plus qu’une petite partie de la théorie logique. Mais pendant longtemps, pour bien des logiciels comme pour Aristote qui en était le principal auteur, ce premier art de bien raisonner qu’était la syllogistique trouvait son fondement dans l’essence même des choses, supposées préexister à la pensée discursive de l’être humain. Dans cette orientation première, la science logique apparaissait ainsi comme le reflet de l’ontologie, de la science de l’être, qui elle-même se reflétait dans le langage par lequel et à travers lequel le logicien et tout être doué de raison rejoignait et saisissait le Vrai. Comme déjà dit, cette dimension avant tout ontologique de la logique perdra peu à peu de sa force, au fur et à mesure que les techniques de raisonnement se multiplieront et que l’étude (scientifique) de la nature se distancera de la vision aristotélicienne du vrai. Mais une chose pourra perdurer: le fait que la logique reste envers et contre tout la science de toutes les formes de raisonnement visant à formuler le vrai ou du moins à conserver, à travers l’enchaînement raisonné des propositions, la valeur de vérité (ou de fausseté, ou de plausibilité etc.) des énoncés une fois celle-ci provisoirement ou durablement admise. En bref, de par cette origine, la logique restera toujours une science normative, qui indique comment procéder, quelle technique de raisonnement adopter, pour être certain que la vérité est conservée à travers les chaînes de raisonnement, aussi longues et complexes soient-elles. Piaget résumera cette dimension normative de la logique en qualifiant cette science de « morale de la pensée ».
Mais dès Leibniz au moins, et surtout à partir du 19e siècle, tout en restant une science du raisonnement vrai, la logique a pris une tournure la rapprochant considérablement du mode pensée proprement mathématique, en donnant naissance à ces disciplines que sont la logique algébrique (manipulant, comme l’algèbre classique, des symboles opératoires exprimant non seulement des propositions ou autres contenus logiques, mais également des opérations logique, ainsi qu’on le verra tout de suite) et la logique mathématique, laquelle se donne entre autres pour tâche de fonder toutes les sciences au sens aujourd’hui accepté du terme « science », et en tout premier lieu les différentes branches des mathématiques (logique incluse) en tant que ces sciences formulent des énoncés et des thèses atteignant, grâce à des méthodes de démonstration elles-mêmes mathématiquement éprouvées, une objectivité et une universalité maximales. Cette nouvelle science logique que constituent la logique algébrique et la logique mathématique ne se présente donc plus, sinon marginalement, comme une science ontologique ni même comme la science de l’art de raisonner correctement. Elle se veut, et est pour une large part, tout à la fois une partie de la science mathématique et son fondement. Si, de la première sorte de logique, Piaget a retenu son caractère profondément normatif (la logique comme « morale de la pensée »), de la seconde il retiendra à la fois, au moins en partie, sa technicité et son projet de fonder les mathématiques, en les adaptant à son propre projet psychologique et épistémologique (l’étude de la genèse du nombre et de l’espace, autour et à partir desquels s’est construite toute la mathématique traditionnelle, des Grecs jusqu’au 19e siècle).
Pour se faire une idée précise de ce qui, dans la nouvelle science logique, a pu jouer un rôle essentiel dans la genèse de la psychologie génétique de Piaget, résumons un petit ouvrage, « L’Algèbre de la logique », cité dans plusieurs de ses écrits et qu’il a lu très certainement avec la plus grande attention lors de son année de formation à Paris, alors qu’il démarrait ses toutes premières recherches sur la pensée logique de l’enfant et de l’adolescent.
Louis Couturat, un des professeurs de Piaget lors de son séjour à Paris, résume dans cet ouvrage publié en 1905 une partie du travail d’axiomatisation et de logicisation des mathématiques (logique incluse) effectué par des auteurs de premier ordre, tels que le mathématicien italien Peano, ou encore les philosophes et mathématiciens anglais Russell et Whitehead (auteurs de ce monument que sont les Principia mathematica, dans lesquels c’est la totalité ou presque de la logique et de la mathématique qui sont présentées, pour chacune de leurs sous-branches comme édifiée sur des nombres réduits d’axiomes, ceci en partie dans le même esprit que, chez Euclide, toute la géométrie était présentée comme pouvant être bâtie sur un nombre réduit d’axiomes, une telle démarche permettant de mettre à l’épreuve la cohérence des disciplines ainsi axiomatisées).
Dans la vision de Russell et Whitehead, que résume donc le petit ouvrage de Couturat, la logique se compose de trois grands domaines: la logique des propositions, la logique des classes et la logique des relations, auxquels correspondent (sous l’angle de l’algèbre à partir duquel ces trois sous-domaines sont considérés) trois calculs partiellement isomorphes, c’est-à-dire plus ou moins complètement traduisibles les uns dans les autres: le calcul des propositions, celui des classes et celui des relations (les deux derniers étant conçus comme des spécialisations du premier, alors que dans l’ordre de la psychogenèse, et comme on le verra, la logique des propositions est plus tardivement maîtrisée que la logique des classes et des relations).
À la base du calcul des classes, comme celui des propositions (ainsi que des relations asymétriques), on trouve chaque fois une unique relation exprimée par le même symbole: « < ». Dans la logique des classes (ou des concepts, celui de fleur correspondant par exemple à la classe des fleurs, la dernière correspondant à l’extension du premier), le symbole « < » exprime l’inclusion d’une classe dans une autre (ou la subsomption d’un concept sous un concept de plus grande extension; exemple: « tulipes < fleurs »). Dans la logique des propositions, le même symbole exprime l’implication (aujourd’hui symbolisée par « ⊃ »; « p < q » exprime le fait qu’une proposition p implique une autre proposition q, par exemple, la proposition « Socrate est un homme » implique la proposition « Socrate est mortel ») [3]. Enfin, en logique des relations asymétriques, la même symbole exprime toute relation asymétrique, par exemple, la relation « plus petit que ».
Une deuxième relation logique de base que l’on retrouve dans les trois calculs est celle d’égalité ou d’équivalence, exprimée par le même signe qu’en arithmétique, soit « = ». Elle peut être définie à partir de « < »: « a = b » si « a < b » et « b < a ». Par exemple, tout triangle équilatéral est un triangle équiangle, et vice versa.
Ce qui précède suffit à montrer que les termes que relient les symboles de base « < » et « = » sont des classes (ou des concepts), des relations asymétriques ou des propositions.
Pour chacun de ces trois calculs, le logicien formule les axiomes, c’est-à-dire les propositions de départ, à partir desquelles toutes les expressions de ces trois calculs se laissent dériver en appliquant les règles qui leur sont propres (de la même façon qu’en arithmétique élémentaire, le mathématicien a mis en exergue les propositions de base à partir desquelles toutes les expressions vraies ou théorèmes arithmétiques se laissent calculer par simple application des règles du calcul arithmétique).
Certains axiomes sont communs aux trois calculs logiques. Par exemple, l’axiome classiquement désigné comme étant le principe d’identité, à savoir: « a < a », dont on peut déduire que « a = a ». Ou encore le principe dit du syllogisme, et qui est fondé sur la transitivité des relations logiques: (a < b) (b < c) < (a < c), d’où peut se tirer l’équation: (a = b)(b = c) < (a = c), soit de a=b et de b=c on peut logiquement, et donc nécessairement, conclure que a=c (pour être cohérent avec la notion précédente concernant la notion d’implication formelle, le symbole qu’il conviendrait d’utiliser ici est donc non pas « < », mais « ⇒ »; mais comme cette distinction n’est pas exposée dans le petit ouvrage de Couturat, nous nous en tenons aux symboles utilisés dans celui-ci, notre propos en le résumant étant avant tout d’illustrer ce qui était vraisemblablement le contexte dans lequel Piaget a développé sa vision de la science logique qui va guider ses recherches de psychologie génétique sur la pensée logique de l’enfant, une pensée dont il va constater qu’elle est voisine des travaux de symbolisation de la logique tels qu’ils sont résumés dans cet ouvrage de 1905, mais qui prennent une forme beaucoup plus précise et développée dans les écrits de Russell, avec lesquels Piaget se familiarisera également très tôt).
Enfin, rapportons encore un dernier pan de cette logique moderne dont Piaget a pu trouver un résumé dans l’ouvrage de Couturat, pan qui en est peut-être le plus important en ce qu’il fait de cette logique une algèbre, à savoir sa dimension opératoire, en d’autres termes la présence d’opérations d’addition et de multiplication logiques telles que Leibniz avait dès le 17e siècle su reconnaître leur similitude avec les opérations propres à l’arithmétique. Voyons à titre d’illustration ce qu’il en est de l’addition logique « x + y = s », définie comme suit par Couturat. Pour un terme x et pour un terme y il existe un terme s pour lequel on a à la fois « x < s » et « y < s » et tel que, pour tout terme z, si x < z et y < z on a aussi s < z. Dans le calcul des classes, de l’addition de deux ou n classes en résulte une autre qui contient ni plus ni moins chacune des deux ou n premières (exemple: l’addition des hommes et des femmes = la classe des humains; or les hommes sont des vertébrés, les femmes aussi, donc les humains le sont) et qui est elle-même contenu dans toute classe (dans cet exemple les vertébrés) contenant la classe des hommes et celles des femmes.[4] Dans le calcul des propositions, l’expression « p + q = r » signifie que l’addition (en d’autres termes le ou non disjonctif aujourd’hui symbolisé par « v ») de deux propositions symbolisées par p ou q est une proposition r qui est impliquée par chacune des deux précédentes et qui implique toute proposition impliquée par celles-ci.
Comme nous le verrons un peu plus loin en examinant quelques-uns des faits recueillis par Piaget dans ses travaux les plus connus sur le développement de la pensée logique concrète de l’enfant, on retrouvera dans l’analyse de ces faits un usage hautement fécond de la logique algébrique comme instrument non seulement de modélisation de ces faits, mais aussi et surtout des structures opératoires sous-jacentes qui expliquent les caractéristiques de la pensée logique concrète telle qu’elle se manifeste à partir de 6-7 ans environ. Mais un bref extrait du livre du premier ouvrage publié par Piaget en 1924 sur « Le jugement et le raisonnement chez l’enfant » révèle comment l’algèbre de la logique a orienté dès le début son approche psychologique de la pensée de l’enfant. Piaget y définit dans les termes suivants ce qu’il conçoit également comme une addition logique de deux classes chez l’enfant: une telle opération « consiste à trouver la plus petite des classes qui les contienne toutes deux », par exemple la classe des animaux pour ce qui est des deux classes que sont les vertébrés et les invertébrés. De même définit-il ce qu’il appelle, à la suite des logiciens, la multiplication logique de deux classes telles que les protestants et les genevois comme étant « l’opération qui consiste à trouver la plus grande des classes qui soit contenues dans ces deux classes à la fois », à savoir les protestants genevois. Ceci paraît assez trivial, néanmoins cette approche tout à fait originale que Piaget adopte en étudiant la pensée de l’enfant se révélera être d’une exceptionnelle fécondité.
Mais avant de présenter avec quelques détails quelques-unes des recherches piagétiennes sur la genèse des opérations logiques chez l’enfant, exposons brièvement quel était l’avancement des recherches sur la pensée de l’enfant dans les années où Piaget a démarré ses propres travaux. Cela nous permettra d’apprécier l’importance et l’originalité de ces derniers.
2. La psychologie
Comme pour la logique, Piaget a bien entendu pris connaissance des travaux réalisés avant lui dans le domaine de la psychologie de l’enfant. Sur ce terrain cependant, les avancées étaient encore rares, la psychologie scientifique n’étant née qu’à la fin du 19e siècle. Un seul auteur avait développé une théorie du développement cognitif de grande profondeur et ampleur (du bébé jusqu’à l’adolescence), à savoir J.-M. Baldwin, qui, comme Piaget, avait vu la pertinence d’établir des liens entre le développement cognitif chez l’enfant et l’évolution des espèces, et plus généralement entre la psychologie et la biologie. Cependant les conceptions développementales de Baldwin, proches à bien des égards de celles que Piaget développera ultérieurement (on y trouve par exemple déjà une place centrale accordée aux notions d’assimilation et d’accommodation), souffrent d’un défaut majeur: si l’on s’en tient aux écrits publiés, elles restent largement théoriques, sans être étroitement reliées à un recueil, une description et une analyse systématiques des faits comme cela sera le cas chez Piaget. Par ailleurs, et contrairement à son jeune collègue, il manque chez Baldwin le bagage très étendu de connaissance acquis par Piaget en épistémologie et en histoire des sciences, ceci en dépit du fait qu’on doit à Baldwin l’invention du terme « épistémologie génétique », mais entendu dans un sens très réduit car ne couvrant, chez lui, que l’étude du développement cognitif de l’enfant, sans interrogations proprement épistémologiques à propos des notions de nombre, d’espace, de temps, de causalité, de quantités physiques, etc. (alors que chez Piaget l’épistémologie génétique, si elle prend un appui crucial sur l’étude du développement cognitif de l’enfant, reste avant tout une science de la science et des notions scientifiques).
Au sein de la psychologie de l’enfant, c’est donc avant tout, et comme déjà signalé lors du premier cours, les travaux portant sur le diagnostic de l’intelligence qui, s’ils n’apportaient qu’un faible éclairage sur la nature de cette dernière, vont fournir à Piaget la clé lui permettant d’accéder au fonctionnement de la pensée de l’enfant. Plus précisément, ils vont l’aider à créer la méthode par laquelle il réussira à percer cette nature. Rappelons en effet que c’est lors de son année de formation passée à Paris entre 1919 et 1921 que Piaget a eu l’opportunité d’interroger des enfants sur des tests de diagnostic de intelligence logique initialement élaborés pour la plupart par le psychologue anglais Cyril Burt et dont le jeune Piaget avait la charge de les étalonner auprès d’enfants de la population parisienne (c’est-à-dire de trouver les âges moyens auxquels les enfants parisiens parvenaient à résoudre des tests d’intelligence de niveaux de difficulté statistiquement différenciés). Mais, et c’est là qu’un vrai changement de paradigme à la fois méthodologique et théorique se produit, au lieu de s’en tenir à ce travail purement statistique d’étalonnage des tests dont Théodore Simon [5] l’avait chargé, Piaget se met à dialoguer avec les enfants qu’il interroge en cherchant à comprendre les raisons de leur échec ou de leur réussite à ces tests qui, envisagés sous ce nouvel angle, sont le point de départ de l’invention de multiples situations-problèmes dont la finalité est d’étudier la genèse de la pensée logico-mathématique et physique chez l’enfant et l’adolescent, et à travers cette étude, de découvrir les racines des sciences logico-mathématiques et de la nature (découverte supposée apporter des réponses scientifiquement fondées à toute une série d’interrogations épistémologiques, dont la plus fondamentale, à savoir celle, kantienne, des conditions de possibilité de ces sciences).
Voilà à titre d’exemples deux des tests de Burt dans leur version simplifiée adoptée par Piaget dans ses premiers travaux sur le développement de la logique chez l’enfant. Le premier concerne la logique des classes et est présenté comme suit à l’enfant: « Jean dit à ses sœurs: “Une partie de mes fleurs sont jaunes”. Puis il leur demande la couleur qu’a son bouquet. Marie dit: “Toutes tes fleurs sont jaunes”. Simone dit: “Quelques-unes de tes fleurs sont jaunes” et Rose dit: “Aucune de tes fleurs n’est jaune” ». « Laquelle a raison ? », demande alors le psychologue à l’enfant.
Et voilà le deuxième problème qui, lui, concerne la logique des relations asymétriques : « Edith est plus blonde que Suzanne. Edith est plus brune que Lili. Laquelle est la plus foncée, Edith, Suzanne ou Lili ? », demande le psychologue à l’enfant. Le problème qui se pose en ce cas à l’enfant est de sortir de la « pseudo-contradiction » que semble être l’attribution à Edith de cheveux simultanément bruns et blonds, ou foncés et clairs. [6] À noter également que ce problème, comme le précédent, est présenté sous une forme purement verbale, ce qui apparaîtra assez rapidement à Piaget être un défaut, ou une complication qui cache l’existence d’une logique plus élémentaire que la logique verbale traditionnelle, dont on retrouve l’emprise jusque dans le caractère primordial accordé par les logiciens modernes à la logique des propositions par rapport à la logique des classes et des relations, défaut auquel Piaget et ses proches collègues psychologues remédieront par l’utilisation d’un matériel concret servant de support aux questions posées aux enfants.
En raison de ce défaut de méthode, je ne m’arrêterai pas ici sur les nombreux résultats auquel a conduit cette première approche de la pensée de l’enfant presque exclusivement utilisée par Piaget lors de sa première décennie de recherches en psychologie. Je signale simplement que c’est seulement vers 10 ans que les enfants parviennent à résoudre de tels problèmes verbaux relevant soit de la logique des classes soit de la logique des relations asymétriques (c’est-à-dire des relations pour lesquelles l’usage du « plus » et du « moins » fait sens). Par la suite, il apparaîtra qu’une manière beaucoup plus concrète de poser les mêmes problèmes permettra aux enfants interrogés de les résoudre dès l’âge de 7-8 ans. C’est ce que l’on verra un peu plus loin, une fois formulées les conclusions que l’on peut tirer de ce bref aperçu du contexte dans lequel Piaget a démarré ses travaux sur la pensée
3. Le contexte des premières recherches: conclusion
Les quelques considérations précédentes suffisent à montrer comment, au départ de son œuvre psychologique, Piaget a abordé le problème du développement cognitif des enfants et des adolescents. Tout en s’appuyant sur les travaux des psychologues de l’enfance du début du 20e siècle, Piaget s’en distancie aussitôt, tant sur le plan des questions qu’il cherche à résoudre et qui sont chez lui tout à la fois épistémologiques et psychologiques, que sur le plan de la méthode mais aussi du cadre théorique qu’il adopte et qui bénéficie de la triple formation acquise par ailleurs par lui en biologie, en épistémologie et en logique. Cependant, à s’en tenir aux contenus des articles et ouvrages publiés dans les années 1920, ses premières recherches psychologiques souffrent, ainsi qu’on vient de le constater, d’un défaut majeur, du moins si on les compare avec ce qui deviendra l’une des caractéristiques principales de la voie d’accès à l’intelligence enfantine. Piaget a en effet démarré son activité psychologique avec « l’idée qui pouvait paraître la plus naturelle en ne connaissant d’avance que la logique adulte […]: c’est que la logique est intimement liée au « discours », et que c’est donc sur le plan du langage ou de la pensée verbale qu’il convenait » d’en entreprendre l’étude (Piaget, 1924, avant-propos de la 3e édition p. 5, daté de juin 1947). Certes, Piaget avait dès le début à l’esprit l’idée que cette logique du jugement et du raisonnement telle qu’elle se manifeste à travers le langage plonge ses racines dans la logique de l’action. Mais dans les années 1920, il pouvait avoir le sentiment que les travaux sur la naissance de l’intelligence sensori-motrice démarrés dès la naissance de son premier enfant, en janvier 1925, suffirait à faire connaître cette logique de l’action. Or l’un des grandes trouvailles de Piaget sera de découvrir très rapidement qu’entre la logique de l’action sensori-motrice et la logique discursive, il existe une pensée concrète mettant en œuvre des opérations logiques portant sur les objets de cette pensée, opérations que l’on peut mettre en correspondance avec celles formalisées par les logiciens, ce qui permettra de résoudre la question du fondement naturel des opérations logiques de classe et de relation, lesquelles pourront être dès lors considérées comme le prolongement, sur le plan de la représentation, des classifications et mises en relation propres à l’activité sensori-motrice, mais un prolongement qui, comme on va le voir, nécessite chez l’enfant toute une reconstruction s’étalant entre 2-3 ans et 9-10 ans (voir à ce sujet les premiers paragraphe de l’avant-propos de la 1ère édition de La genèse du nombre chez l’enfant, de 1941). Cette découverte d’une forme concrète de pensée logique précédant la logique discursive résulte de la conscience acquise très tôt chez Piaget (dès 1926-27, voire avant) que pour mettre à jour la pensée logique de l’enfant, la méthode d’entretien clinique visant le seul échange verbal entre enfant et adulte ne suffit pas et qu’il conviendrait de compléter les échanges verbaux en confrontant l’enfant à des problèmes concrets, impliquant des objets pouvant être manipulés par lui. Un passage de son livre de 1927 sur La causalité physique chez l’enfant est très clair à ce sujet et mérite d’être cité presque in extenso. Piaget y décrit trois méthodes qui peuvent être utilisées lors d’un entretien clinique avec les enfants conduit, en l’occurrence, dans le but de connaître leur conception de la causalité:
Les méthodes qui se proposent à nous […] sont au nombre de trois, de valeur très inégale, mais qu’il importe cependant d’employer concurremment, pour être sûr de ne rien laisser échapper d’intéressant. La première est une méthode toute verbale : demander aux enfants si les corps [physiques] ont de la force et pourquoi. L’on obtient ainsi la définition ou la notion verbale de la force. La seconde est une méthode mi-verbale, mi-concrète : on énumère à l’enfant un certain nombre de mouvements (celui des nuages, des ruisseaux, des pièces d’une machine, etc.) et l’on demande le pourquoi et le comment de ces mouvements. […] Enfin la troisième méthode est directe, autant que faire se peut: on institue devant l’enfant, quelques petites expériences de physique et l’on demande le pourquoi de chaque événement. On obtient ainsi des renseignements de première main sur l’orientation d’esprit des enfants. (pp. 3-4)
Ce qu’affirme ici Piaget peut bien entendu être généralisé à toute recherche visant à connaître les particularités de la pensée de l’enfant. Transposée à la situation d’examen de la pensée logique de l’enfant, la deuxième méthode est celle qui a été utilisée avec les tests de Burt dont il a été question précédemment et dans lesquels il s’agissait pour les enfants interrogés de décider des réponses correctes à donner à un problème logique énoncé verbalement.
Ce que révèle également ce passage ainsi que d’autres se trouvant dans les publications des années 1920, c’est que, si tous les résultats rapportés par Piaget dans celles-ci sont toujours basés sur une méthode soit purement verbale, soit, comme il le dit, sur une méthode mi-verbal, mi-concrète (le concret en question restant néanmoins toujours présenté sur le seul plan verbal), certains travaux sont déjà en cours dont les résultats feront quelques années plus tard éclater les conclusions tirées de cette approche « mi-verbale, mi-concrète » (en réalité encore beaucoup trop verbale !), mais travaux en cours dont Piaget ne prend alors pas conscience de la refonte qu’ils exigeront de sa conception première des rapports entre la logique de l’action et la logique de la pensée chez l’enfant. Il faudra attendre les années trente pour que l’usage de cette troisième méthode et le grand nombre de faits inattendus et révélateurs auquel va conduire le recours à des objets bien réels conduisent à mettre en lumière la structure originale de la pensée de l’enfant telle qu’elle émerge non pas vers 9-10 ans, comme le laissaient croire les réponses des enfants aux tests de Burt, mais dès 6-7 ans Certes, l’usage de l’approche verbale a pu déjà apporter des résultats importants en ce qui concerne les particularités de cette pensée, notamment le passage d’une forme « égocentrée » à une forme de pensée décentrée apte à coordonner entre eux des jugements formulés à partir de différents points de vue (ce processus de décentration reproduisant sur le plan du développement de la pensée de l’enfant le processus parallèlement observés lors du développement de l’intelligence sensori-motrice). Mais cette approche verbale passe à côté d’un fait majeur qui prendra toute son importance dans les années 1930: que l’enfant de 7-8 ans ne puisse pas résoudre sur le plan verbal des problèmes de logique tel que ceux rencontrés dans les tests de Burt ne signifie pas qu’il n’ait pas déjà construit les opérations propres à cette logique des classes et à celle des relations asymétriques formalisée par Russell, Whitehead et d’autres logiciens mathématiciens, opérations qui interviennent à côté d’autres, plus abstraites, dans la résolution de ces problèmes. Les faits recueillis par Piaget et ses collègues au moyen de la troisième des méthode d’entretien clinique vont en effet révéler que l’enfant n’a pas besoin d’attendre 9-10 ans ou 10-11 ans (voir Piaget, 1924, p. 93) pour résoudre des problèmes de logique des classes ou de logique des relations asymétriques; il pourra les résoudre deux ou trois années plus tôt pour autant qu’il puisse juger et raisonner en s’appuyant sur du matériel concret (ou en certains cas sur des images le représentant fidèlement et qui puissent être elles-mêmes manipulées en lieu et place des objets représentés).
* * * * *
II. Le développement de la logique des classes
Afin d’illustrer le développement des opérations liées à la logique des classes chez l’enfant, nous allons examiner la progression des réponses des enfants à deux types de problèmes créés par Piaget et ses collègues. Le premier type concerne l’activité de rangement d’objets de toute nature communément à l’œuvre dans la vie de tous les jours. Réussir à réunir et donc à classer pratiquement des objets n’implique cependant pas encore la pleine acquisition de l’opération de base la plus commune de cette logique des classes: à savoir l’addition logique, en d’autres termes l’inclusion de classes et, puisqu’il s’agit d’addition, la quantification qui l’accompagne, c’est-à-dire le fait de savoir qu’une classe logique contient nécessairement plus d’éléments que n’importe laquelle de ses sous-classes, sauf cas tout à fait exceptionnel tel qu’on pourrait le rencontrer sur le terrain de la classification naturelle des espèces. [7] C’est pour étudier le développement de l’addition logique qu’un second type de problème a donc été conçu qui, lui, porte explicitement sur la quantification logique liée à la maîtrise de cette opération et donc de l’inclusion logique. Le premier type de problème pouvant être résolu sans recourir à des opérations logiques pleinement acquises, mais de manière empirique, nous ne ferons que le présenter succinctement, le seul intérêt de cette présentation étant de décrire des types différents d’activité de rangement d’objets qui s’échelonnent entre 2-3 ans et 6 ans environ.
Problème I: la classification d’objets de formes, de grandeurs et de couleurs différentes
Dans ce premier type de problème de classification, on montre à l’enfant toute une série hétéroclite d’objets placés devant lui en lui demandant de « mettre ensemble ce qui va ensemble », ou de « mettre ensemble les choses qui vont bien ensemble ».[8] Comme les critères sur lesquels l’enfant peut s’appuyer peuvent être très nombreux et consister non pas seulement sur de multiples critères de ressemblance entre objets (par exemple ranger des animaux avec d’autres animaux, ou ranger des objets en fonction de leurs formes géométriques, de grandeurs clairement différenciées —petit, moyen, grand—, de couleurs également clairement distinctes les unes des autres —rouge, vert, bleu, etc.—) mais sur des critères tout aussi multiples de convenance (par exemple, mettre ensemble une ferme et des animaux que l’on peut généralement y trouver), on peut demander à l’enfant de ranger les objets qui vont bien ensemble dans deux ou trois boîtes que l’on place devant lui. Confrontés à ce genre de problème, les enfants présentent trois types successifs de réponse. À un premier niveau, vers l’âge de 3 ans environ, lorsqu’il s’agit sans autres de « mettre ensemble les objets qui sont pareils », ou « les mêmes », etc., les enfants font intervenir pêle-mêle les critères de ressemblance et de convenance. Confrontés à une situation où on leur présente des formes géométriques de grandeurs et de couleurs différentes, ils pourront par exemple les rassembler en formes de contours rectilignes d’un côté, en formes de contours curvilignes de l’autre, etc., mais de manière à ce que chaque collection présente en outre une forme particulière (par exemple une maison pour les objets de formes rectilignes).
Lors d’une deuxième étape, vers 5-6 ans, on voit disparaître l’utilisation des critères de convenance. L’enfant s’efforce de construire des collections selon les seuls critères de ressemblance et de différence (une ferme sera rangée avec d’autres bâtiments, les animaux de ferme avec d’autres animaux, etc.), mais il peut sans raison apparente changer de critères de ressemblance au cours de son activité de rangement, passant par exemple, pour les objets de formes, de grandeurs ou de couleurs différentes, d’un critère de forme à un critère de couleur ou de grandeur. Les enfants les plus avancés de ce niveau peuvent aussi construire des sous-collections d’objets à l’intérieur d’un ensemble d’objets jugés aller ensemble. Ainsi, un enfant ayant posés des formes rondes d’un côté et des formes carrées de l’autre pourra à l’intérieur de chacun de ces deux groupes séparer les formes carrées en sous-groupes selon leur couleur, ou bien selon leur grandeur. Ces enfants se rapprochent alors des conduites de classification telles qu’on peut les observer lors de la troisième étape lors de laquelle collection et sous-collections seront construites selon un ordre précis et constant dans le choix des critères (par exemple, la forme, puis la grandeur, puis la couleur). Cependant, si on pose aux enfants du deuxième niveau des problèmes de quantification quant aux collections et sous-collections qu’ils ont construites (par exemple à la question de savoir s’il y a plus, moins ou la même chose de carrés rouges que de carrés, ils se révèlent incapables de concevoir la relation d’inclusion qu’implique l’opération d’addition logique et qui seule permet de répondre correctement). Le troisième niveau étant celui d’une juste compréhension de la relation d’inclusion, il convient de considérer le deuxième type de problèmes et les réponses que les enfants leur apportent pour saisir comment, à ce niveau, le sujet parvient à résoudre logiquement, c’est-à-dire opératoirement et déductivement —et non pas, comme chez certains enfants les plus avancés du deuxième niveau, de manière opportuniste et en manifestant un malaise intellectuel (on en verra un exemple)— les problèmes de classification logique, et du coup à formuler des jugements logiquement fondés face aux questions de quantification logique qu’on lui soumet.
Problème II: l’inclusion des classes et la quantification logique
Pour illustrer les comportements des enfants confrontés à ce deuxième type de problème de logique qui ciblent directement le développement de la quantification logique des classes, nous allons présenter les comportements des enfants face à deux situations utilisées par Piaget et Szeminska dans leur recherche sur la genèse du nombre dans ses rapports avec celle de la logique des classes et des relations (GdN, chap. II) [9].
1ère illustration: le problème des perles.
Le problème posé à des enfants de 4 à 10 ans est le suivant. On montre au sujet une boîte ouverte dans laquelle se trouve une vingtaine de perles en bois, dont 16 ou 17 brunes et les autres blanches. Après lui avoir fait constater que toutes les perles sont en bois, on pose alors au sujet la question standard suivante [10] : « est-ce que, dans cette boîte, il y a plus de perles brunes, plus de perles en bois ou la même chose ? » (l’ordre de présentation entre les trois choix de réponses possibles peut bien sûr varier). La réponse tout aussi standard des enfants les plus jeunes est alors « il y a plus de perles brunes » ! On verra tout à l’heure l’interprétation que donne Piaget de cette erreur absolument générale chez les enfants les plus jeunes (sauf bien sûr si un adulte leur a appris à répondre correctement, mais il suffira de modifier un peu l’épreuve pour qu’un enfant drillé à répondre correctement fournisse une réponse standard, c’est-à-dire erronée, mais plus conforme à ses propres capacités [11]). Notons également que ce même problème posé à des enfants en moyenne un peu plus âgés se verra immédiatement résolu de manière tout à fait correcte, avec une justification sans faille consistant à affirmer qu’il y a plus de perles en bois puisque parmi celles-ci il y a non seulement des brunes mais également des blanches (autrement dit, en termes de calcul des classes, que B, la collection des perles en bois, contient plus d’éléments que la collection A des perles brunes, puisque B = A+A’, avec A’ désignant les éléments de B qui ne sont pas inclus dans la collection A).
Des questions complémentaires sont ensuite posées aux enfants qui jugent qu’il y plus de perles brunes que de perles en bois pour s’assurer que c’est bien là ce qu’ils pensent. Le psychologue commence par poser la question suivante: « si un enfant décide de prendre toutes les perles brunes pour en fait un collier, alors qu’un autre enfant décide de prendre toutes les perles en bois, est-ce que l’un des deux aura un plus long collier, ou bien les colliers auront-ils la même longueur ? ». Voilà la réponse donnée par un enfant de 6 ans 8 mois à cette nouvelle question, réponse qui est cohérente avec son affirmation précédente: le plus grand collier est celui fait avec les perles brunes. Le psychologue demande alors à cet enfant de dessiner les deux colliers, le premier dessin représentant le collier avec toutes les perles en bois, le deuxième dessin toutes les perles brunes. Une fois les deux dessins correctement réalisés (le premier dessin « contenant » donc correctement toutes les brunes et toutes les blanches, et le deuxième toutes les brunes), le psychologue demande alors à nouveau au sujet lequel des deux colliers sera le plus long, celui qui contient toutes les perles en bois, ou celui contenant toutes les brunes. Chez cet enfant de 6 ans et 8 mois, la cohérence est maintenue: le collier des perles brunes est toujours jugé être le plus long. Cette cohérence des réponses est caractéristique du premier stade: les enfants de ce niveau ne changent pas leur réponse, quand bien même ils savent tous que les perles blanches sont aussi des perles en bois et que le collier des perles en bois est composé des perles brunes et des perles blanches.
Le même problème peut être posé sous des formes légèrement différentes à d’autres enfants (ces variations sont exposées dans l’ouvrage sur La genèse du nombre mentionné précédemment). Quelle que soit la forme sous laquelle il l’est, à chaque fois on retrouve la même incapacité des enfants du premier stade à comparer les quantités respectives d’éléments d’une classe et de l’une de ses sous-classes.
A titre illustratif, prenons un deuxième exemple de comportement de ce premier stade, cette fois observé chez un enfant de 7 ans et 3 mois, donc un peu plus âgé et qui lui aussi affirme, en réponse à la question standard, qu’il y a plus de perles brunes que de perles en bois. A la suite de cette réponse, le psychologue dessine les perles brunes et les perles blanches sur une feuille puis demande à l’enfant de tracer au crayon un cercle autour des brunes. L’enfant le fait sans difficulté. Le psychologue lui demande ensuite de tracer un cercle autour des perles en bois. Cet enfant trace alors un cercle autour des seules perles blanches, comme si le fait d’avoir tracé un cercle autour des brunes excluait de pouvoir les inclure dans l’ensemble des perles en bois ! Le psychologue demande alors innocemment à cet enfant si les perles brunes ne sont pas elles aussi en bois. Le sujet l’admet sans difficulté. Il efface alors le cercle tracé autour des seules perles blanches et trace un cercle autour des toutes les perles en bois. Vient alors à nouveau la question standard de savoir s’il y a plus, moins ou la même chose de perles en bois ou de perles brunes. Cet enfant de 7 ans et 3 mois n’en continue pas moins à affirmer qu’il y a plus de perles en bois que de brunes, alors même que, sous ses yeux, le cercle autour des perles en bois inclut le cercle des perles brunes ! Chez d’autres enfants de cet âge ou un peu plus âgé, de telles questions complémentaires à celle de départ peuvent finir par les ébranler dans leur jugement. Ils peuvent alors osciller entre une réponse correcte et leur réponse initiale, ou formuler non sans hésitation un jugement définitivement correct mais non logiquement justifié, ce qui révèle une progression de leur pensée logique, l’accès à un stade intermédiaire de développement, l’incertitude qu’ils conservent montrant toutefois que l’opération d’addition de classe n’est pas complètement acquise chez eux.
Pour cerner de plus près ce qu’implique la maîtrise complète de l’opération de base de la logique des classes chez les enfants, examinons la progression des réponses des enfants confrontés à un problème similaire, mais portant cette fois sur la classification des fleurs, classification plus naturelle que reflète la langage (par les noms différents donnés à différentes espèces florales).
2eme illustration: l’inclusion des fleurs.
Dans cet autre problème, un enfant a devant lui un dessin représentant un pré avec des fleurs, soit une vingtaine de coquelicots et 3 bleuets (dans un des exemples que nous exposerons, ce matériel sera remplacé par un bouquet de fleurs en plastique, des roses et des œillets). On commence par demander à l’enfant de décrire ce qu’il voit et qu’il reconnaît sans difficulté être des fleurs. On lui apprend éventuellement que les rouges sont des coquelicots, les bleus des bleuets, puis on lui pose la question standard suivante: « dans ce pré, si on veut faire un très gros bouquet de fleurs, est-ce qu’il faut cueillir toutes les fleurs ou tous les coquelicots ? ». Les réponses des enfants peuvent être classées en trois stades selon qu’ils affirment sans hésitation qu’il faut cueillir tous les coquelicots, ou alors qu’après avoir donné cette réponse erronée, ils en viennent à formuler la réponse correcte, ou enfin que d’emblée ils affirment, avec justification à l’appui, que, nécessairement, le bouquet composé avec toutes les fleurs est plus grand que celui composé avec tous les coquelicots.
Voyons des exemples de ces trois étapes, et d’abord la première illustrée par les réponses d’une fillette de 5 ans (GdN, p. 213). Après qu’il se soit assuré qu’elle reconnaît les espèces de fleurs présentées, l’expérimentateur lui pose la question de savoir si, pour faire le plus gros bouquet, il faut prendre toutes les fleurs ou tous les coquelicots. « Les coquelicots », répond-elle. L’expérimentateur lui demande alors de montrer les coquelicots, ce qu’elle fait correctement, puis de montrer toutes les fleurs. Elle répond là aussi correctement en faisant un geste circulaire autour de toutes les fleurs. On lui pose alors à nouveau la question standard, en réponse à laquelle elle s’exclame: « mais je te l’ai déjà dit » !
Le deuxième exemple illustre le comportement du deuxième stade d’une fillette de 6-7 ans, Anouchka, (nous n’avons pas d’indication sur son âge exact) interrogée par Gérald Nœlting, collaborateur de Bärbel Inhelder, dans le cadre des recherches longitudinales sur le développement de la pensée logique chez l’enfant.[12] Dans ce cas, les coquelicots et les bleuets dessinés sur une feuille sont remplacés par 5 roses et 2 œillets en plastique. L’expérimentateur commence par demander à l’enfant de montrer les roses dans le bouquet. Elle les montre une à une. Après qu’elle a également montré les deux œillets (dont elle apprend alors le nom), l’expérimentateur lui demande de montrer toutes les fleurs du bouquet. Après une petite hésitation, elle montre toutes les fleurs une à une. Ensuite, on lui pose la question standard de savoir s’il y a plus de fleurs ou plus de roses. Ce à quoi elle commence par répondre immédiatement, donc sans trop réfléchir: « il y en a autant » (en négligeant donc la présence des œillets), en esquissant spontanément une justification « oui, parce que… » qu’elle interrompt soudainement pour affirmer: « non, il y a plus de roses ! ». « Explique-moi —lui demande l’adulte— il y a plus de roses que de quoi ? » « Que de… que d’œillets », répond-elle un brin embarrassée. « Oui —confirme le psychologue— il y a plus de roses que d’œillets ! Mais ce que moi je te demande, c’est s’il y a plus de roses ou plus de fleurs ! ». « Mais les fleurs, c’est les œillets », riposte-t-elle, toujours un peu embarrassée, à quoi elle ajoute, après un petit temps d’arrêt: « et puis les roses aussi ». « C’est ça », dit l’adulte, en se tournant vers l’enfant pour relancer la question: « alors, finalement, qu’est-ce que tu crois ? » (qu’il ne complète pas, jugeant que l’enfant a encore en tête la question standard qu’il vient de lui rappeler). Réponse d’Anouchka: « Il y a plus de roses, parce que… » (elle ne parvient pas à compléter sa justification). Après une petite pause, l’entretien redémarre au point de départ, avec une petite modification de la question standard (aide involontairement donnée à l’enfant avec l’usage de la notion de comptage): « Dans ce bouquet, si je compte toutes les fleurs et si je compte toutes les roses, est-ce qu’il y a plus de fleurs ou plus de roses ? ». Anouchka devient manifestement perplexe. Elle se tourne vers l’adulte pour lui demander, sous une forme mi-affirmative, mi-interrogative et tout en passant sa main sur la totalité du bouquet: « Mais les fleurs, c’est ça ! ? ». Après confirmation, Anouchka et l’adulte se mettent à nouveau d’accord, comme au début de l’entretien, pour dire qu’une partie des fleurs sont des œillets, qu’une autre ce sont des roses, et que tout le bouquet, « ce sont des fleurs, des œillets et des roses », précise l’enfant. L’expérimentateur reconnaît que le problème qu’il pose n’est pas facile, qu’il fait réfléchir. Il demande à nouveau à Anouchka: « finalement, il y a plus de fleurs ou plus de roses ». Anouchka manifeste une certaine irritation en répondant: « mais pourquoi tu les appelles des fleurs ? ce sont des œillets ! ». Sa réponse indique que pour elle il n’est pas possible de comparer la quantité de fleurs et la quantité d’œillets. L’expérimentateur confirme que les deux fleurs que la fillette pointe du doigt sont en effet des œillets et qu’en effet il y a plus de roses que d’œillets, mais la question est de savoir s’il y a plus de roses ou plus de fleurs. Le problème paraît un instant insoluble et la fillette oscille dans son effort de comprendre ce que sont les fleurs: « Mais les fleurs c’est… c’est tout ça », dit-elle à nouveau en passant sa main sur tout le bouquet, et en ajoutant: « il y en a autant », « parce que ça aussi c’est des fleurs » (les deux œillets). Finalement, une autre perche tendue par l’adulte va permettre à l’enfant de trouver une solution à ce problème qui l’embarrasse. Il lui demande: « si par exemple je voulais donner à ta maman toutes les fleurs, ou plutôt, non, je vais lui donner qu’un bouquet de roses », quel bouquet serait le plus grand. Anouchka réfléchit un moment, et lorsque l’adulte lui repose la question: « quel serait le bouquet le plus grand, le bouquet des fleurs ou le bouquet des roses », elle répond: « le bouquet de fleurs, de tout ça » (elle passe sa main sur toutes les fleurs). Et sa réponse à la question « pourquoi serait-il plus grand » confirme dans une certaine mesure l’affirmation selon laquelle le bouquet de fleurs est plus grand: « parce que si on en enlève 2, il en restera 3, il ne peut pas en rester 5 ». L’entretien se termine par la reconnaissance, chez Anouchka, que le bouquet le plus grand, « c’est celui des fleurs », sans que l’on sache trop si à ce moment Anouchka a en vue la totalité du bouquet (ce que suggère son geste couvrant l’ensemble des fleurs) ou seulement la partie composée des roses (ce que suggère partiellement sa justification arithmétique dans laquelle il est question d’enlever 2 fleurs à 5 fleurs=roses et non pas à 7 fleurs).
Ce qui précède est une claire manifestation du deuxième stade, dans lequel Anouchka se confronte au problème de comparaison entre les extensions d’une classe et de l’une de ses sous-classes. Si elle parvient finalement à répondre correctement à un tel problème, c’est de manière encore toute intuitive, en prenant appui sur deux intuitions empruntées l’une à l’espace (la grandeur comparée du bouquet total et de l’une de ses parties) l’autre à un début d’arithmétisation du problème. Concernant ce deuxième appui, elle sait certes que si on enlève des éléments à une collection composée d’un petit nombre d’élément, ce qui restera sera un moins grand nombre d’éléments, mais l’usage de l’arithmétique qu’elle fait ici pour répondre à un problème de quantification logique reste lui-même intuitif et problématique, et de plus elle réduit de nombre de fleurs du bouquet au nombre de roses.
Quant aux réponses des enfants du troisième stade (qui ont en moyenne 9-10 ans), elles ne prêtent plus à aucune équivoque. Un enfant de ce stade affirmera sans hésiter qu’il y a nécessairement plus de fleurs dans le bouquet de fleurs composé de coquelicots et de bleuets que dans le bouquet composé des coquelicots. Il reste à savoir pourquoi ce qui s’impose avec évidence au troisième stade pose problème au deuxième stade et n’est même pas envisageable au premier stade.
La quantification logique et la construction de l’opération additive des classes
Pour Piaget, la réponse à la question précédente tient dans la capacité qu’ont les enfants du 3e stade de pouvoir penser simultanément à une partie incluse dans un tout et à ce tout en tant qu’incluant cette partie, et un tel pouvoir est la conséquence directe de la construction et de la maîtrise de l’opération d’inclusion ou d’addition logique. Avant ce stade, l’enfant ne parvient pas ou (voir le cas d’Anouchka) seulement avec beaucoup de peine et en prenant appui sur des indices non-logiques (la frontière du bouquet de fleurs, ou bien une corde entourant la classe totale des perles en bois versus une corde entourant l’une de ses sous-classes) à concevoir simultanément la classe totale avec ses deux sous-classes, ainsi que l’une ou l’autre des deux sous-classes.
D’un côté, si l’enfant se centre sur une sous-classe A et qu’on lui demande de concevoir simultanément la classe totale B (composée de A et des éléments de B qui ne sont pas des A), il réduira systématiquement celle-ci à la partie complémentaire A’ de cette sous-classe (les bleuets, si la sous-classe mentionnée est celle des coquelicots). Avec une telle réduction de la classe totale B à la complémentaire A’ de A, la difficulté disparaît lorsque les collections comparée contiennent un nombre pas trop élevé d’éléments: un enfant de 4 à 6 ans sait comparer les numérosités perceptives respectives de deux petites collections d’objets (ce qui ne veut pas dire qu’il maîtrise la notion de nombre, comme on le verra dans le prochain cours). Comme dans le cas d’Anouchka, il voit bien que telle espèce de fleurs est plus nombreuse que telle autre espèce appartenant au même bouquet de fleurs.
Et d’un autre côté, si on l’incite à penser à la classe totale B, il parviendra certes à résoudre des questions qui ne concernent que le tout (par exemple lorsqu’on lui demande de faire un cercle autour de toutes les fleurs); mais aussitôt qu’on lui demande de comparer quantitativement ce tout avec l’une de ses parties A, il lui sera impossible de séparer en pensée cette partie de ce tout sans du même coup ne plus pouvoir penser le tout !
À une certaine étape de progression de ses capacités cognitives cependant, il cherchera, comme Anouchka, à penser à la fois au tout et à l’une de ses parties, mais ses réponses oscilleront entre une réponse ou une autre (l’une réduisant le tout B à une de ses deux parties, soit A’, pour comparer sa numérosité à celle de A, l’autre en comparant sans le réduire, ce même tout B à sa partie A, mais alors en s’appuyant sur des indices spatiaux), en marquant un embarras d’autant plus grand que la conscience du problème s’accroît.
Enfin viendra le moment où il comprendra d’emblée que le tout n’est rien d’autre que la somme de ses parties, que chacune des parties n’est rien d’autre que le même tout, mais soustrait de toutes les autres parties qui ensemble composent la complémentaire de cette partie relativement à la totalité des éléments en jeu, et du coup, une question dans laquelle on lui demande comparer un tout à l’une de ses parties ne lui pose plus aucun problème, la solution s’imposant à ses yeux avec la plus grande évidence (si B = A1+A2, alors B est nécessairement quantitativement plus grand aussi bien de A1 que de A2, pour autant bien sûr que ni A1 et ni A2 ne soient pas des collections vides).[13]
Par la suite, l’explication livrée par Piaget trouvera certes des contradicteurs. Certains affirmeront que tout est affaire d’attention ou d’extension du champ d’attention. Mais Piaget avait déjà noté en 1922, à l’occasion de ses premières recherches sur la pensée logique des enfants, que ce type d’explication n’est pas satisfaisant: un enfant peut bien penser à deux choses à la fois, par exemple aux quantités respectives d’éléments de deux sous-classes, sans que pour autant il parvienne à penser simultanément aux quantités respectives d’éléments d’une totalité et de l’une de ses sous-classes. Ce n’est pas un problème d’attention qui est en jeu, mais un problème de conception des classes logiques découlant de l’absence de construction des opérations additives de classe nécessaires à la mise en relation des quantités respectives des éléments d’une classe et de l’une de ses sous-classes.
D’autres contradicteurs évoqueront un problème d’apprentissage du langage (du français par exemple): les jeunes enfants ne comprennent pas qu’on puisse leur demander de comparer quantitativement une classe à sa sous-classe (voir la réaction d’Anouchka, qui tend à rejeter la question qu’on lui pose). C’est exact, mais cela n’explique là aussi en rien pourquoi une question qui paraît inconcevable à un jeune enfant ne soulève plus aucun problème quelques mois ou quelques années plus tard, voire, comme chez Anouchka, au cours même d’un entretien de « maïeutique constructiviste », sinon parce que ses notions de tous et de quelques, de classes et de sous-classes ont progressé de manière à rendre possible et même évident ce qui était auparavant rejeté (question y comprise).
Avec l’addition des classes logiques et son inverse, la soustraction logique, toutes deux complétées par l’opération de multiplication des classes qui permet par exemple à un enfant de croiser deux classifications d’une même collection d’objets pouvant être de formes géométriques de différentes espèces (carrées, rondes, triangulaires, etc.) et de différentes couleurs (rouges, bleues, vertes, etc.) et par son inverse, la division ou abstraction logique, qui permet de concevoir les formes carrées abstraction faite de leur différence de couleur, c’est l’un des deux aspects de la logique concrète que parvient à maîtriser l’enfant entre 7 et 9 ans. Voyons maintenant ce qu’il en est de la deuxième grande classe d’opérations logiques concrètes également maîtrisée entre 7 et 9 ans environ, à savoir celles qui concernent non plus la logique des classes, c’est-à-dire les opérations portant sur la réunion ou la séparation d’éléments selon telle ou telle de leur qualité, mais celles des relations logiques asymétriques, qui concernent la mise en ordre croissant ou décroissant d’une collection d’éléments selon telle ou telle de leur dimension, ou, en d’autres termes, non plus la classification logique, mais la sériation logique.
III. Le développement de la logique des relations asymétriques
A noter tout d’abord que les relations logiques incluent non seulement les relations asymétriques, mais également les relations symétriques, en particulier la relation d’équivalence ou d’égalité, qui est sous-jacente à la logique des classes (ce qu’indique d’ailleurs le symbole « = » utilisé dans le calcul des classes). Notons que certaines propriétés sont communes aux relations symétriques et aux relations asymétriques, comme par exemple la transitivité logique : après avoir constaté que a=b (c’est-à-dire vérifié que tous les éléments rouges d’une collection sont grands et tous les grands de la même collection sont rouges) et b=c (tous les éléments rouges de la même collection sont carrés et tous les carrés rouges) l’enfant qui a acquis les opérations de la logique des classes et auquel on cache cette collection n’en déduira pas moins immédiatement ou après une brève réflexion que, nécessairement, il y a autant de grands que de carrés, soit a=c. Il en va de même en logique des relations asymétriques: de ce que a<b et b<c, un enfant qui maîtrise le calcul de ces relations déduira immédiatement et nécessairement que a<c.
Remarquons encore, pour poursuivre ce dernier exemple et comme le souligne Piaget, que ce n’est pas parce qu’un enfant de 2 ans ou de 3 ans peut reconnaître et affirmer que tel objet est plus lourd que tel autre (ou tel garçon plus grand que lui-même), qu’il a construit et maîtrise l’opération de sériation logique et la notion de relation de grandeur. Plus précisément, un enfant de cet âge ne peut pas, après avoir constaté que A est plus lourd (ou plus grand) que B, puis que B est plus lourd (ou plus grand) que C en déduire que A est plus lourd (ou plus grand) que C. À la question de savoir lequel est le plus lourd ou le plus grand il répondra qu’ « on ne peut savoir à l’avance, qu’il faut peser ou regarder pour le savoir ». L’intérêt des recherches réalisées par Piaget et Szeminska sur le développement de la sériation logique et qui sont exposées également dans un des chapitres (le 5e) de l’ouvrage sur La genèse du nombre chez l’enfant est de révéler le cheminement que suit l’enfant pour atteindre le niveau de compétence lui permettant de résoudre un problème qui nous paraît trivial, cheminement qui passe là aussi par la construction des opérations additives et multiplicatives portant non plus sur des réunions ou des séparations, mais sur les différences entre les éléments comparés lors de leur mise en ordre.
Enfin, dernière remarque préalable, tout ceci peut paraître ne concerner qu’une faible partie de l’activité intellectuelle de l’enfant. Mais une brève réflexion permet de se déprendre d’une telle réserve. De même que les opérations de classe interviennent constamment et inconsciemment dans la vie de l’enfant en lui permettant à l’enfant de ranger les objets et événements du monde selon leur similitude, et d’emboîter les classes ainsi composées les unes dans les autres (les événement sportifs avec les événements sportifs, les événements culturels avec les événements culturels, etc.), de même ne cessent-ils pas de sérier les objets selon telle ou telle de leur dimension (ce qui trouve d’ailleurs un écho dans le langage, avec l’usage fréquent, mais pas toujours logique, des expressions telles que « plus grand que », « plus fort que », etc. En un mot, même si on n’en prend en général que peu conscience, la logique des opérations concrètes ne cesse d’intervenir dans nos activités communes et si chaque individu ne parvenait pas à acquérir les opérations qui la compose, les échanges avec le monde extérieur et avec nos pairs seraient hautement problématiques.
Mais venons-en au fait en commençant par exposer les stades d’acquisition de la sériation logique ou de l’addition des relations asymétriques avant d’exposer les stades de la multiplication de ces mêmes relations.
L’addition des relations asymétriques
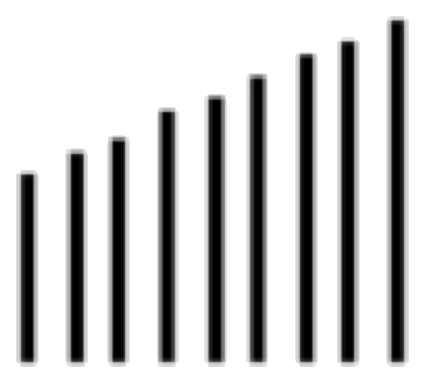
L’épreuve standard permettant de révéler l’acquisition progressive de cette opération qui est au cœur de la logique des relations asymétriques porte sur la sériation d’une collection d’une dizaine de baguettes dont chacune est de grandeur différente. Après avoir montré aux enfants individuellement interrogés un dessin représentant cette dizaine de baguettes donc chacune a successivement 10 cm de plus que l’autre et qui sont disposées de manière à former un escalier (voir la figure 1), on leur donne les dix baguettes bien réelles en les priant de bien vouloir les ranger pour que cela fasse un escalier « comme sur le dessin ». Comme dans le cas du problème de l’inclusion des fleurs, les réponses des enfants peuvent être rangées en trois stades.
1er stade: le rangement des baguettes par couples ou triplets
Les enfants en moyenne les plus jeunes construisent des couples ou des triplets sans les coordonner entre eux et sans respecter la ligne de base, ce qui donnent des productions telles que celles-ci (à noter que si l’on demande aux enfants non pas de sérier de vraies baguettes, mais de dessiner l’escalier, ils pourront résoudre plus vite cette épreuve, mais non sans passer par des étapes similaires). La figure ci-dessous schématise les réponses données par les enfants de ce stade:
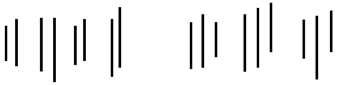
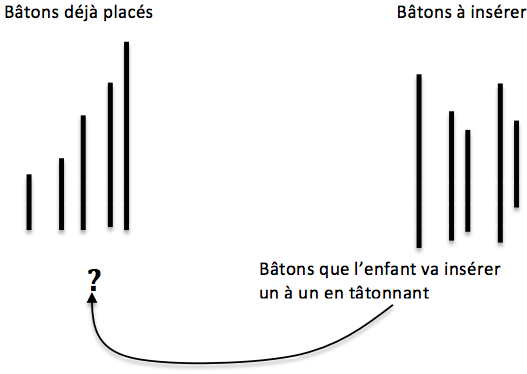
2ème stade: une méthode empirique de sériation
Un enfant ayant atteint ce niveau parvient à construire une sériation conforme au modèle, mais de manière empirique (de même qu’un bébé du 5ème stade du sensori-moteur parvenait à résoudre par tâtonnement des problèmes d’intelligence pratique tel que celui de faire passer un bâton à l’intérieur d’un parc d’enfant). Il commence par exemple par placer correctement 4 ou 5 bâtons en les choisissant par simple estimation perceptive, pour prendre ensuite successivement dans n’importe quel ordre chacune des baguettes restantes en l’insérant par tâtonnement dans la série déjà construite et dont il redistribue alors si nécessaire les éléments qui la compose, un procédé empirique que schématise là aussi la figure suivante:
3ème stade (vers 7 ans): une méthode opératoire de sériation
A ce dernier niveau, l’enfant parvient d’un seul coup à construire la série entière, au moyen d’un procédé qu’il invente tout seul avant même de commencer à placer une seule baguette, ou après avoir commencé à placer par estimation perceptive la plus grande ou les deux plus grandes baguettes de la collection initiale, procédé qui implique une compréhension complète de la notion (relative) de longueur et des opérations qui relient les unes aux autres chacune des différences en jeu. Cette méthode consiste à se saisir récursivement de l’ensemble de toutes les baguettes restantes (et en premier lieu de toutes les baguettes s’il commence d’emblée à utiliser ce procédé), de poser, sans les lâcher, cet ensemble verticalement sur la table, de s’emparer de la plus grande baguette pour la placer à gauche de la série de celles qui ont déjà été placées sur la table pour réaliser l’escalier demandé, et de répéter le même procédé jusqu’à ce que l’ensemble de baguettes restantes soit vide:
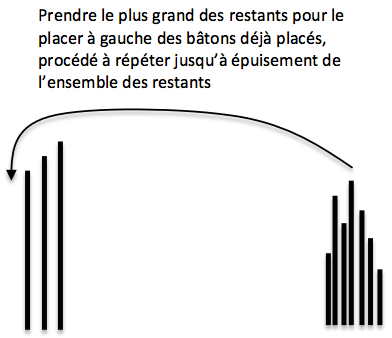
Contrairement à la méthode empirique utilisée par les enfants du stade 2, un enfant du 3ème stade sait d’emblée qu’en prenant le bâton le plus grand de tous les restants, ce bâton sera nécessairement, une fois placé dans la série ascendante en construction, le plus petit des bâtons déjà placés. Il a donc à l’esprit l’ensemble des relations asymétriques en jeu, et il sait qu’à chaque étape du processus, la différence s’accroitra entre le premier et le tout dernier des bâtons placés.
A noter cependant que ce procédé opératoire utilisé par les enfants de ce 3ème stade implique que ces enfants aient par ailleurs construit la notion opératoire de longueur: le déplacement d’un objet dans l’espace ne modifie en rien sa longueur. D’autres recherches portant sur la construction de cette notion révèlent que chez les enfants les plus jeunes, le simple déplacement d’un objet dans l’espace ne garantit en rien la conservation des longueurs. C’est la raison pour laquelle la logique des relations asymétriques que l’enfant acquiert entre 6-7 et 9 ans environ est une logique concrète, c’est-à-dire toujours liée aux notions attachées aux objets concrètement manipulés par les enfants. Il suffit donc de modifier les objets ou les caractéristiques des objets sur lesquels les enfants agissent pour que le savoir opératoire acquis en tel ou tel domaine (ici la sériation des longueurs) ne le soit pas nécessairement en un autre domaine (celui de la sériation d’objets de poids différents par exemple, la notion opératoire de poids étant plus tardivement acquise que celle de longueur).
Mais revenons au seul problème de la sériation des longueurs. On vient de voir que l’enfant du 3ème stade découvre le procédé lui permettant de résoudre opératoirement et non pas empiriquement ce problème, procédé déduit de ce savoir selon lequel, en procédant du plus grand vers le plus petit, chaque élément d’une série succède à ses précédents et précède ses suivants (ou vice versa si l’on procède du plus petit au plus grand). En d’autres termes, il coordonne entre elles « les relations ascendantes et les relations descendantes » (Piaget, Epistémologie de la relation, in L’évolution humaine, Flammarion, 1957, p. 161 [14]). On constate ici la présence d’une propriété fondamentale d’une pensée devenue opératoire, c’est-à-dire capable de concevoir ses objets au moyen d’opérations logico-mathématiques telles que l’addition des différences, à savoir la réversibilité: à toute opération directe correspond une opération inverse; en l’occurrence, à l’addition d’une différence correspond la soustraction de cette différence addition et soustraction permettant de circuler dans les deux sens dans une série d’objets de longueurs différentes comme de concevoir simultanément que si un objet est plus grand qu’un autre, nécessairement cet autre est plus petit que le premier.
Notons également que l’addition des relations asymétriques est plus simple à acquérir et à mettre en œuvre que l’addition des classes (avec le problème du rapport entre partie et tout qui la concerne). En effet, si on reprend l’exemple de la sériation des baguettes, le matériel utilisé permet de constater intuitivement que la différence entre la 3ème baguette et la 1ère contient la différence entre la 1ère et la 2e, et la question fait d’emblée sens de comparer la troisième (ou la quatrième ou la cinquième) à la première, et non pas seulement la deuxième à la troisième (alors que de comparer la quantité de fleurs à la quantité de roses paraît absurde tant que l’on n’a pas acquis la notion opératoire d’inclusion logique): d’où l’acquisition plus précoce, au moins dans des cas tels que celui de la sériation des baguettes, de l’addition des relations asymétriques, par rapport à celle de la quantification des classes. Il n’empêche que cette saisie intuitive ne prend tout son sens que lorsque l’enfant est capable d’additionner et de soustraire les différences. C’est alors seulement, en effet, que cet enfant sait d’emblée que chaque nouvelle baguette dont il se saisit vient avant les plus grandes déjà placées et après les plus petites qu’il restera à placer. D’où il peut déduire que la somme des différences successives est égale à la différence qui sépare la première des baguettes de celle qu’il est en train de poser. Et d’où il peut également déduire, sans obligation de vérification empirique, que si on constate que si telle baguette est plus grande qu’une deuxième, et si l’on constate par ailleurs que celle-ci est plus petite qu’une troisième, alors nécessairement la première est plus grande que la troisième. Mais il suffit de poser un problème concernant les relations asymétriques dans un contexte tel que celui de la sériation d’objets de poids différents où aucun appui n’est possible sur une intuition empirique immédiate pour que la maîtrise opératoire de ces relations ne devienne accessible qu’au même âge où le devient l’opération apparemment plus abstraite de quantification liée à l’addition des classes (soit vers 9 ans), et cela alors même que la modélisation des opérations en jeu dans l’un et dans l’autre cas aboutisse à un modèle algébrique strictement isomorphe.
Pour terminer cet exposé forcément incomplet sur le développement de opérations logiques concrètes chez l’enfant entre 5 et 9 ans, examinons encore le cas non plus de l’addition mais de la multiplication des relations asymétriques.
La multiplication des relations asymétriques
Commentons brièvement au moyen de deux exemples les étapes franchies par les enfants pour acquérir cette opération de multiplication logique des relations asymétriques (nous retrouverons un problème voisin lors du 9ème cours portant sur la construction du nombre chez l’enfant).
Le premier exemple concerne la double sériation de deux collections d’images dont les unes représentent les niveaux successifs d’un liquide contenu dans un premier récipient et se déversant dans un second récipient, et les autres les niveaux correspondant de liquide remplissant le second récipient au fur et à mesure que le premier se vide.
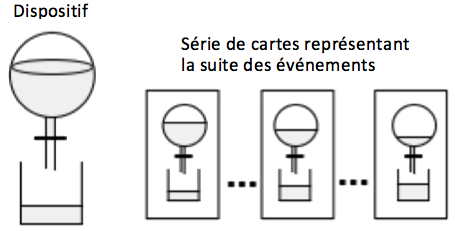
Dans un premier temps, on donne en désordre à l’enfant les cartes représentant la suite des événements (voir figure ci-dessus, qui représentent le dispositif ainsi que la série ordonnée des cartes représentant cette suite) en lui demandant d’ordonner ces cartes pour qu’une fois sériées elles représentent ce qui se passe au fur et à mesure que le liquide s’écoule.
Les stades que franchissent les enfants pour répondre à ce problème de simple sériation correspondent à celles observées dans la sériation des bâtons de différentes longueurs. C’est également vers 7 ans en moyenne que les enfants réussissent ce problème de sériation logique.
Dans un second temps, on donne à l’enfant non plus non plus les cartes sur lesquelles sont représentées simultanément le niveau du liquide dans le vase et le niveau de liquide dans le verre dans lequel il s’écoule, mais deux collections de cartes dont l’une représente en désordre quelques niveaux du vase qui se vide, et l’autre, également dans le désordre, les niveaux du verre qui se remplit (voir l’illustration ci-dessous qui montre la double sériation correctement ordonnée).
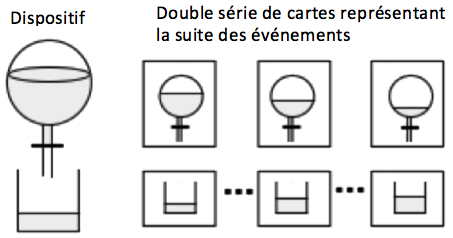
Ce que suggèrent les réponses des enfants à ce deuxième problème, c’est que celui-ci, en apparence plus compliqué car exigeant pour sa résolution non seulement le recours à l’addition de relations asymétriques mais également à la multiplication de deux séries de relations asymétriques, peut être résolu dès que le premier l’est. Ceci pour autant toutefois que le problème consiste seulement à mettre en relation, d’un côté des niveaux d’eau successifs dans le verre qui se vide, avec des niveaux d’eau successifs dans le verre qui se remplit, sans que l’enfant ait à résoudre des problèmes de simultanéité temporelle et ait à considérer les vitesses différentes avec lesquels les niveaux s’abaissent ou s’élèvent dans les deux verres [15]).
Quant au deuxième exemple, il concerne un problème où, contrairement au premier, il n’existe pas de correspondance naturelle entre les deux relations à multiplier l’une avec l’autre. Dans ce problème, on place en vrac devant l’enfant des images représentant des feuilles d’arbre donc chacune peut être petite, moyenne ou grande, ainsi que de teinte claire, moyenne ou foncée. Le problème que l’enfant va devoir résoudre est de ranger toutes ces feuilles selon un ordre de tailles croissantes et selon un ordre de teintes également croissantes. Ce problème en apparence plus compliqué que le premier confirme qu’aussitôt qu’un enfant sait effectuer une mise en ordre selon une seule des deux dimensions (la taille ou bien la teinte), il sait le faire pour les deux critères de taille et de teinte. Pour les enfants, cette capacité de double sériation (donc de multiplication de deux séries ordonnées) ne soulèvent pas plus de problème que la seule capacité de construire une simple sériation, et ceci quand bien même la double sériation porte non pas, comme dans le premier exemple, entre des éléments isolés et naturellement reliés (le vase qui se vide et le verre qui se remplit), mais sur un même ensemble d’éléments à classer selon l’une ou l’autre des deux dimensions considérées et qui n’ont aucun lien naturel évident (des classes de feuilles de trois couleurs différentes, et les mêmes feuilles pouvant être rangées dans trois classes de tailles différentes).
Examinons plus en détail ce deuxième problème de multiplication des relations asymétriques portant non plus sur des éléments isolés quoique reliés, mais des classes d’éléments qu’il s’agit de ranger selon deux sortes de relation asymétrique (la taille et la teinte).
Soit trois grandeurs de feuilles d’arbres I, II et III, et trois teintes croissantes 1, 2, 3.
Pour résoudre le problème de classification selon les deux dimensions il faut avoir simultanément[16] à l’esprit qu’il ne convient pas seulement de ranger les feuilles soit selon leur taille soit selon leur teinte, mais qu’il faut faire en même temps les deux choses. C’est avec une telle exigence à l’esprit que l’enfant va donc tout à la fois rechercher les petites feuilles qu’il va ranger dans l’ordre croissant des trois teintes, les feuilles de grandeur moyenne qu’il va également ranger dans l’ordre croissant des teintes et enfin les grandes feuilles selon le même critère de teinte croissante. Ce faisant, il va produire un tableau de classification à double entrée qui prend la forme suivante:
| I1 | → | I2 | → | I3 |
| ↓ | ↓ | ↓ | ||
| II1 | → | II2 | → | |
| ↓ | ↓ | ↓ | ||
| III1 | → | III2 | → | III3 |
En d’autres termes, alors qu’un enfant de niveau préopératoire n’aura pas à l’esprit de s’en tenir aux seules petites feuilles pour les ranger selon les trois teintes, puis aux seuls moyennes feuilles pour les ranger selon leur teinte, pour finir seulement par ranger les seules grandes feuilles selon leur teinte et ainsi aboutir à résoudre le problème de double sériation, et qu’il procédera au mieux de manière empirique mais sans parvenir à une solution finale satisfaisante, un enfant de niveau opératoire aura la précaution de procéder d’emblée en coordonnant c’est-à-dire en multipliant les deux relations d’ordre dont il aura la certitude dès le départ qu’elle insérera chacun des éléments en jeu dans la place qui lui revient logiquement et non pas seulement empiriquement.
Enfin notons que cette symbolisation de ce que réalise un enfant lorsqu’il parvient à résoudre ce problème apparemment plus complexe de multiplication des deux relations asymétriques révèle comment cette multiplication n’est rien d’autre qu’une mise en correspondance de deux additions de relations asymétriques, ce qui permet de comprendre pourquoi un enfant qui a construit l’opération d’addition logique des relations n’a pas de peine à résoudre simultanément ou après un bref tâtonnement un problème de multiplication revenant à chaque fois à croiser ou coordonner l’addition des différences propres à la première relation (différences symbolisées par les flèches du tableau ci-dessus) avec l’addition des différences propres à la deuxième relation (ou à la troisième, etc., s’il y en a plus que deux).
* * * * *
Je vais arrêter là cette analyse logique des opérations additives et multiplicatives au moyen desquelles les enfants de 6-7 à 9 ans parviennent à résoudre les problèmes logiques auxquels les confrontent les chercheurs en psychologie génétique, non sans mentionner une nouvelle fois que ces opérations qui apparaissent sous une forme particulièrement épurée dans le contexte de ces recherches piagétiennes n’en sont pas moins constamment utilisées dans la vie de tous les jours pour classer ou ranger des objets, ainsi que concevoir les relations logiques que ces objets entretiennent les uns avec les autres.
J’ajouterai seulement, et sans entrer dans le détail, les deux remarques suivantes:
1° La formalisation que l’on peut faire des groupements d’opération de classification ou de sériation révèlent que ces groupements (par exemple celui de l’addition des classes, avec son inverse, la soustraction logique des classes) obéissent à des lois ou révèlent des propriétés mathématiques précises. Ce que Piaget résume dans les termes suivants: « la pensée de l’enfant ne devient logique que par l’organisation de systèmes d’opérations obéissant à des lois d’ensemble communes », à savoir: i. la loi de composition (deux opérations d’un ensemble peuvent toujours se composer entre elles et donner comme produit une opération de l’ensemble); ii. la réversibilité (toute opération de l’ensemble peut être inversée, ce que l’on a vu aussi bien en logique des classes qu’en logique des relations; iii. L’opération directe d’un ensemble composée avec son inverse donne une opération nulle ou identique: ajouter la classe des humains puis la soustraire de la classe des animaux revient à laisser identique cette dernière. Ces trois lois valent aussi bien pour l’arithmétique que pour la logique des classes et des relations; mais certaines lois ne valent plus que pour ces dernières, notamment iv. celle dite de tautologie qui concerne l’existence en logique d’opérations identiques spéciales: additionner la classe des humains à la classe des humains revient à additionner la classe des humains, alors qu’en arithmétique additionner un nombre puis additionner à nouveau ce nombre ne revient pas à additionner une seule fois ce nombre. L’existence de ces lois propres à la seule logique des classes et des relations justifie le fait que Piaget appelle « groupement » les regroupements opératoires d’opérations logiques, et qu’il réserve le nom de « groupe » aux structures d’opérations dont les lois ne connaissent pas les limitations propres aux groupements logiques.
2° L’analyse cette fois non plus logique des groupements d’opérations logiques montre que les lois algébriques dégagées par l’analyse logique ont une réelle portée psychologique. Par exemple, lorsque le sujet ayant atteint le niveau opératoire compose des opérations logiques (ou arithmétiques, ou géométriques), il sait qu’il peut toujours les inverser (ou les annuler), non pas en se souvenant du point de départ (ce qui ne garantit pas une inversion logique), mais en effectuant en ordre inverse les transformations précédemment effectuées. Ce savoir d’une opération d’inversion toujours logiquement et psychologiquement possible (pour autant que le sujet ait conservé la trace des opérations effectuées) permet ainsi d’éviter de devoir se souvenir de l’enchaînement de tous nos états de conscience, une mémorisation d’ailleurs psychologiquement impossible. Le sujet sait en outre que, sauf erreur d’attention et non respect des règles logiques, toute déduction ou calcul réalisé à l’intérieur d’un champ opératoire aboutit à des conclusions ou des résultats certains.
_________________________
[1] Rappelons —et ceci est important— que cette activité intentionnelle de coordination des moyens et des fins ne remplace pas mais complète des processus plus élémentaires d’accommodation, de différenciation et de coordination (non-intentionnelle) des schèmes d’assimilation pouvant eux aussi donner naissance à de nouveaux schèmes sur lesquels la coordination intentionnelle des moyens et des fins pourra s’appuyer.
[2] La logique du vivant. Une histoire de l’hérédité. Paris, Gallimard, 1970. François Jacob est, aux côtés de Jacques Monod et André Lwoff, l’un des trois biologistes à qui l’on doit la découverte de l’ARN messager en 1960, c’est-à-dire les molécules qui transmettent au sein du cytoplasme l’information contenue dans les gènes.
[3] L’exposé que donne Couturat du calcul logique et des notions qui le composent est simplifié et lacunaire par rapport au calcul que des auteurs tels que Russell et Whitehead sont en train de développer. La notion d’implication, par exemple, est chez ces auteurs l’objet d’une analyse qui les conduit à distinguer une notion dite matérielle d’implication, correspondant à l’usage courant de l’implication tel qu’il est illustré ici par ce qui est dit de Socrate (soit un usage qui se rattache très directement à la notion d’inclusion logique) de la notion d’implication formelle, qui lie nécessairement des propositions les unes aux autres, dans la mesure où elles obéissent à des lois logiques. Alors, après tout, qu’il n’est pas logiquement nécessaire que Socrate soit mortel (sauf du point de vue aristotélicien d’une ontologie métaphysique qui admet l’existence d’essences logiques telles que celle de l’humain), la proposition « p ⊃ r » est nécessairement, c’est-à-dire logiquement vraie s’il est vrai que les propositions « p ⊃ q » et « q ⊃ r » le sont, ce qui en termes de logique mathématique s’écrit: « (p ⊃ q) et (q ⊃ r) ⇒ (p ⊃ r) », le symbole « ⇒ » exprimant l’implication formelle, qui relie des propositions, alors que, malgré les apparences, l’implication commune porte sur les rapports logiques des contenus de deux propositions telles que Socrate est un homme et Socrate est mortel.
[4] Tout ceci paraît à première vue hautement abstrait et bien peu psychologique. Néanmoins de telles opérations logiques sous-tendent la plupart de nos conduites, comme par exemple lorsque nous rangeons des assiettes ensemble et que nous mettons cet ensemble en un lieu regroupant non pas des habits, mais d’autres couverts de table (par exemple des verres, des tasses, etc.). La logique que nous mettons alors en œuvre n’est plus seulement une logique de l’action, mais une logique de la pensée, basée sur des opérations qui nous permettent de mettre en relation les classes en question.
[5] T. Simon était le collègue et successeur d’Alfred Binet (décédé en 1912), l’un des pères fondateurs d’un test de diagnostic de l’intelligence chez l’enfant toujours utilisé, sous une forme régulièrement révisée, en psychologie appliquée. Binet avait par ailleurs réalisé plusieurs recherches sur le fonctionnement de l’intelligence chez l’enfant, mais sans parvenir à en percer la structure.
[6] Cette pseudo-contradiction naît de la fausse assimilation de la propriété relative qu’est le fait d’être plus ou moins clair ou plus ou moins brun à une propriété absolue telle que celle d’être un nombre positif ou au contraire un nombre négatif : un nombre ne peut pas être simultanément positif ou négatif; il est soit l’un soit l’autre, et dire qu’un nombre peut être plus positif ou plus négatif qu’un autre n’a aucun sens. Cette assimilation erronée, chez un sujet, d’une propriété relative à une propriété absolue est un indice de la non-maitrise, chez lui, de la logique des relations.
[7] Dans le cas de la classification des espèces en biologie, il peut arriver (du moins si l’on en croit ce qu’écrit le naturaliste et logicien Piaget dans ses ouvrages de logique) qu’une sous-classe contenue dans une classe de niveau supérieur contienne autant d’éléments, ni plus ni moins, que la classe qui l’inclut en contient. Cela n’est cependant biologiquement possible que lorsque la classe de rang supérieur ne contient (du moins en l’état actuel des découvertes biologiques) qu’une seule sous-classe ! Comme ce type de situation ne se rencontre pas dans la vie commune (laquelle, contrairement à la taxonomie biologique, ne distingue pas de multiples niveaux de classification très bien déterminés, à savoir espèces, genres, familles, ordres, classes, embranchements, règnes), nous nous limiterons à ne considérer le problème de la quantification logique que dans le cas où le nombre de sous-classes d’une classe logique ne se réduit pas à une seule sous-classe (à noter qu’en biologie le terme de « classe » désigne un rang bien déterminé de la hiérarchie des formes, celui compris entre les ordres et les embranchements; dans le présent texte, « classe » doit bien entendu être compris dans le seul sens logique, et non pas dans le sens biologique).
[8] Les recherches de ce premier type sont présentées dans un ouvrage de 1959 sur La genèse des structures logiques élémentaires, qui complète les chapitres de l’ouvrage de 1941 sur La genèse du nombre chez l’enfant portant sur les opérations logiques élémentaires, dont l’inclusion ou l’addition logique.
[9] Le prochain cours sur la genèse du nombre chez l’enfant explicitera les raisons pour lesquelles une étude sur le développement de la quantification logique a été réalisée en lien avec la recherche sur le nombre.
[10] À noter: cette question standard porte sur la quantité logique et non pas sur la quantité arithmétique des deux collections d’éléments en jeu (bien qu’un lien relie nécessairement la seconde notion à la première, l’inverse n’étant pas vrai : savoir qu’il y a arithmétiquement plus de pommes rouges que de pommes vertes dans deux collections de pommes ne permet pas de conclure que la quantité logique de la première collection est plus grande que celle de la seconde ; en fait, il n’existe aucun rapport de quantité logique entre la collection des pommes rouges et celles des pommes vertes.
[11] Nous ne pouvons pas approfondir ici ce point pourtant essentiel de la conception piagétienne de l’intelligence, conception qui correspond, sur le terrain du développement psychologique, à la distinction entre adaptation phénotypique et plus superficielle, dans laquelle prédomine l’action du milieu sur la forme d’un organe d’un être vivant, et adaptation génotypique plus profonde dans laquelle il y peut y avoir réorganisation durable des déterminants internes de la forme du même organe). Brièvement dit, sur le terrain de l’intelligence, singer Einstein n’est pas le comprendre. Le comprendre, c’est reconstruire les déterminants cognitifs internes de sa théorie physique, ou plus simplement reconstruire celle-ci (et non pas l’apprendre par cœur).
[12] Les réponses d’Anouchka que nous présentons ici sont extraites d’une vidéo qui peut être consultée sur le site de la Fondation Jean Piaget, à l’adresse URL suivante:
http://www.fondationjeanpiaget.ch/fjp/site/ModuleFJP001/index_gen_page.php?IDPAGE=79&IDMODULE=44
[13] A noter que l’exercice intellectuel que nous réalisons ici afin de traduire sous forme de symboles les opérations de pensée de l’enfant met en œuvre, sur un plan certes plus abstrait, le même processus d’abstraction et de réflexion que celui qu’Anouchka doit accomplir pour progresser dans les réponses qu’elle apporte au problème impliqué dans les questions du psychologue qui l’interroge. En d’autres termes, elle est amenée à penser ce qu’elle accomplit spontanément lorsqu’elle conçoit le bouquet en tant que composé par des roses et des œillets.
[14] Texte disponible sur le site de la Fondation Jean Piaget.
[15] Lorsque le problème fait explicitement intervenir des questions de vitesse et de temporalité, l’enfant qui parvient vers 7 ans à résoudre séparément les deux sériations puis à les mettre en correspondance en s’appuyant sur la sériation des hauteurs, ne parvient à coordonner opératoirement les deux série d’images que vers 9 ans (ce décalage s’expliquant par la complexité propre aux notions opératoire de vitesse et de temps; voir à ce sujet le 1er chapitre de l’ouvrage de Piaget sur Le développement de la notion de temps chez l’enfant)!
[16] À noter que, contrairement au problème précédent, le sujet n’a pas à maitriser —donc à penser— opératoirement la notion de simultanéité (et donc à composer des mouvements de vitesse différente) pour réussir cette opération de multiplication logique, mais à opérer simultanément une double classification, ce qui n’est pas la même chose!